
第七节函数的连续性函数的连续性的概念、二、函数的间断点三、初等函数的连续性四、小结思考题高等数学(上册)
一 、函数的连续性的概念 二、函数的间断点 四、小结 思考题 第七节 函数的连续性 三、初等函数的连续性

函数连续性的概念x<0x设 f(x)0xx>0x-1如上图,函数在点x三0处显然间断,即不连续。而下列函数曲线却在每一点连续yy=sint高等数学(上册)
y x 1 1 o 1, 0 ( ) 1, 0 x x f x x x 设 函数连续性的概念 y sin t t y

同学们画出下面两个函数的图像,并观察这两个函数的图像有什么本质的不同?x,x>0x,x≥0f(x) =1,x= 0g(x)-x,x<o-x,x<o请同学们从严格的理论上解释该不同,高等数学(上册)
同学们画出下面两个函数的图像,并观察 这两个函数的图像有什么本质的不同? , 0 , 0 ( ) 1, 0 ( ) , 0 , 0 x x x x f x x g x x x x x 请同学们从严格的理论上解释该不同

函数的连续性(continuity)一1.函数的增量(increment)设变量u从它的初值u,变到终值u,则Au=u,-ui称为变量 u的增量注意:(1)△u可正可负;(2)△u 是一个整体,不能看作 △与u的乘积。高等数学(上册)
一、函数的连续性(continuity) 1.函数的增量(increment) . 2 1 1 2 称为变量 的增量 设变量 从它的初值 变到终值 则 u u u u u u u 注意:(1) u 可正可负; . (2) 与 的乘积 是一个整体,不能看作 u u
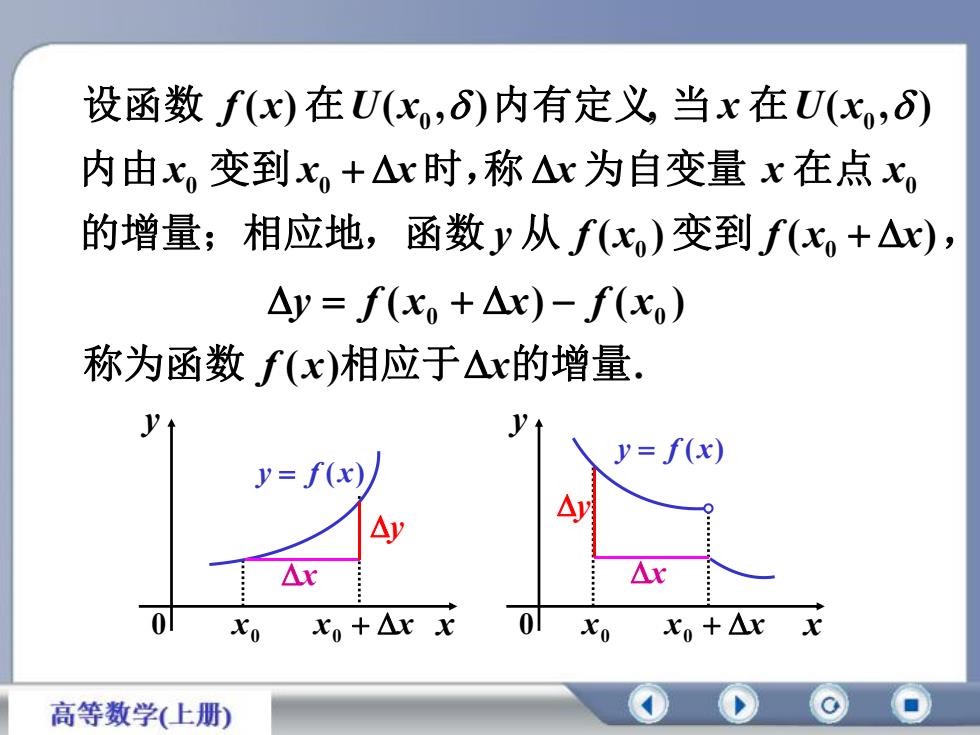
设函数 f(x)在U(x,)内有定义 当x在U(x,)内由x变到x+△x时,称Ax为自变量 x在点x的增量;相应地,函数y从f(x)变到f(x+△x)Ay = f(xo + Ax) - f(xo)称为函数 f(x)相应于△x的增量,yyy= f(x)y= f(x)AyAyArAxo10lXo + Ar xXo + Arxxoxo高等数学(上册)
的增量;相应地,函数 从 变到 , 内由 变到 时,称 为自变量 在点 设函数 在 内有定义 当 在 ( ) ( ) ( ) ( , ) , ( , ) 0 0 0 0 0 0 0 y f x f x x x x x x x x f x U x x U x ( ) . ( ) ( ) 0 0 称为函数 f x 相应于 x的增量 y f x x f x x y 0 x y 0 0 x x x 0 y f ( x) x 0 x x x 0 x y y y f ( x)