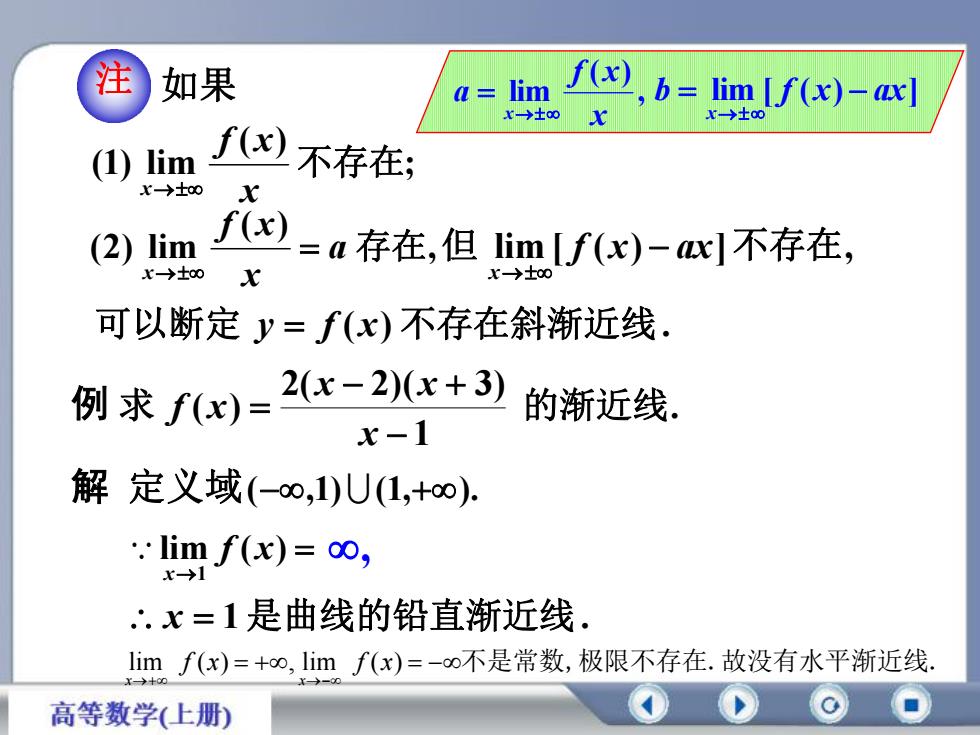
注f(x)如果b=limlf(x)-axllima=→±-→士00Xf(x)不存在;(1)limx-→±xf(x)a 存在,但 lim[f(x)一ax]不存在,(2) limx-→±ox→±0x可以断定=f(x)不存在斜渐近线。2(x - 2)(x + 3)例求f(x)=的渐近线。x-1解 定义域(-0,1)U(1,+),: lim f(x)= 00,x-→1x=1是曲线的铅直渐近线。lim f(x)=+0,lim f(x)=-o不是常数,极限不存在.故没有水平渐近线家高等数学(上册)
; ( ) (1) lim 不存在 x f x x , ( ) (2) lim a 存在 x f x x 可以断定 y f ( x) 不存在斜渐近线. 例 . 1 2( 2)( 3) 求 ( ) 的渐近线 x x x f x 解 (,1)(1,). 注 lim ( ) 1 f x x , x 1是曲线的铅直渐近线. 如果 但 lim [ f ( x) ax]不存在, x b lim [ f (x) ax] x , ( ) lim x f x a x 定义域 lim ( ) , lim ( ) x x f x f x 不是常数,极限不存在.故没有水平渐近线

2(x-2)(x+3)的渐近线。求 f(x):x-12f(x)b= lim[f(x)-ax]a=lim线limX-→±8士8x→0f(x)2(x - 2)(x + 3)=2=a又: limlimx(x -1)X-→00xX-→00lim[f(x) - ax] =lim[f(x) -2x]x>8x802(x - 2)(x + 3)-2xl= limlx-1x-→2(x - 2)(x + 3) - 2x(x -1)4=b= limx-1X-→00:y=2x+4是曲线的一条斜渐近线。C高等数学(上册)
x f x x ( ) 又lim ( 1) 2( 2)( 3) lim x x x x x 2 2 ] 1 2( 2)( 3) lim[ x x x x x 1 2( 2)( 3) 2 ( 1) lim x x x x x x 4 y 2x 4 是曲线的一条斜渐近线 . 1 2( 2)( 3) lim x x x x 无水平渐近线 lim[ f (x) ax] x . 1 2( 2)( 3) 求 ( ) 的渐近线 x x x f x lim[ f (x) 2x] x b lim [ f (x) ax] x , ( ) lim x f x a x a b