
第四节隐函数及由参数方程所确定的函数的导数隐函数的导数、二、 E由参数方程所确定的函数的导数三、小结思考题高等数学(上册)
一 、隐函数的导数 三、小结 思考题 二、由参数方程所确定的 函数的导数 第四节 隐函数及由参数方程 所确定的函数的导数

一、隐函数的导数(differentiation of functions represented implicitly)定义:由方程F(x,)=O所确定的函数=(x)称为隐函数y=f(x)形式称为显函数,F(x,y)=0 →隐函数的显化y=f(x)高等数学(上册)
一、隐函数的导数 定义: . ( , ) 0 ( ) 称为隐函数 由方程F x y 所确定的函数 y y x y f (x) 形式称为显函数. F(x, y) 0 y f (x) 隐函数的显化 (differentiation of functions represented implicitly)
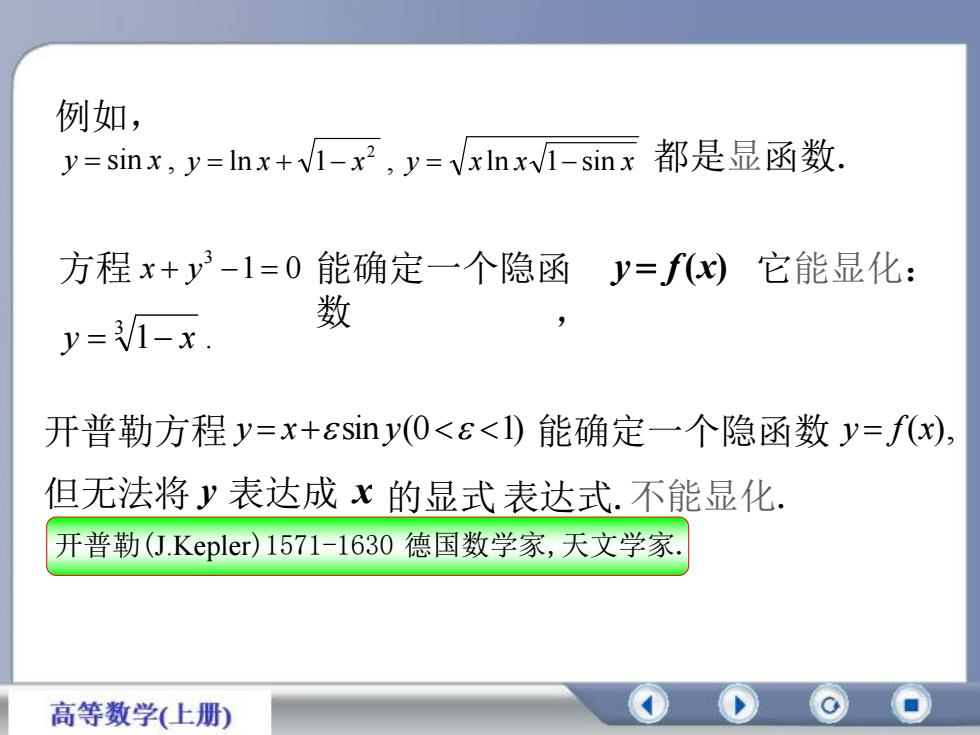
例如,都是显函数y=sinx,y=lnx+/1-x?,y=xlnx/1-sinx方程x+y3-1=0 能确定一个隐函y=f(x) 它能显化:数y=3/1-x.开普勒方程=x+sin(O<<l)能确定一个隐函数=f(x),但无法将y表达成x的显式表达式.不能显化开普勒J.Kepler)1571-1630德国数学家,天文学家高等数学(上册)
例如, y sin x , ln 1 , 2 y x x y x ln x 1 sin x 都是显函数. 方程 1 0 3 x y 它能显化: 1 . 3 y x 开普勒方程 y x sin y(0 1) 但无法将 y 表达成 x 的显式 表达式.不能显化. 开普勒(J.Kepler)1571-1630 德国数学家,天文学家. 能确定一个隐函数 y f(x), 能确定一个隐函 数 , y f(x)
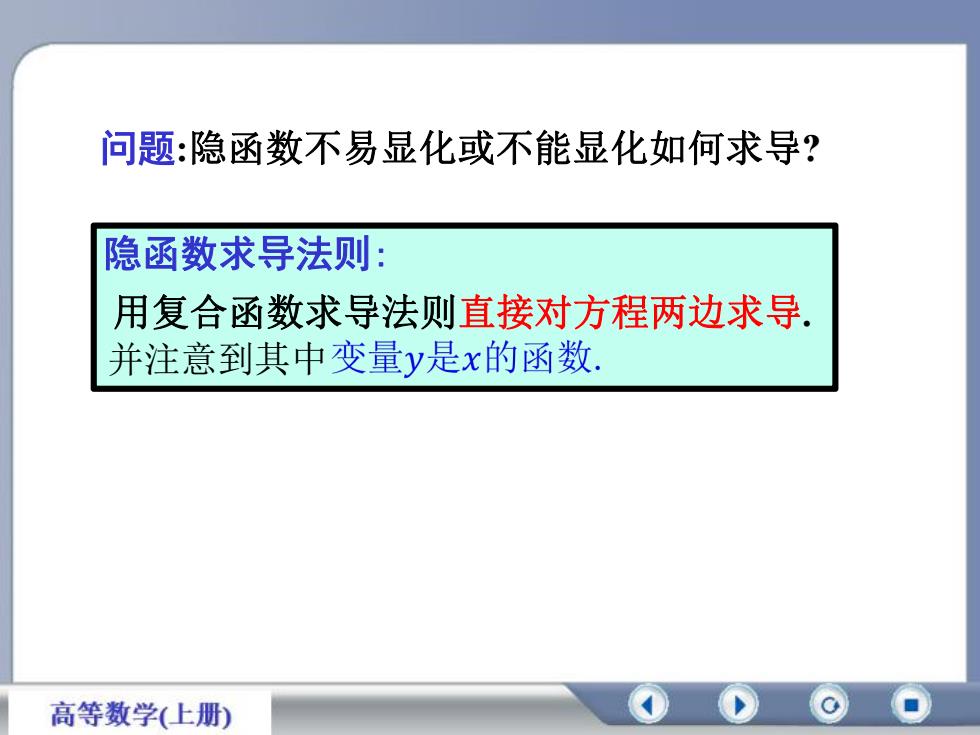
问题:隐函数不易显化或不能显化如何求导?隐函数求导法则:用复合函数求导法则直接对方程两边求导并注意到其中变量V是x的函数高等数学(上册)
问题:隐函数不易显化或不能显化如何求导? 隐函数求导法则: 用复合函数求导法则直接对方程两边求导. 并注意到其中

例1 求由方程呈xy-ex+e=0所确定的隐函数dy, dyy的导数1x=0dx'dx解方程两边对x求导dy01y+xdxdxex-ydy解得x=0代入原方程=y=0x+eydxdyey=1.-x=0x=0esdxx+y=0高等数学(上册)
例1 . d d , d d 0 0 x x y x y x y y xy e e 的导数 求由方程 所确定的隐函数 解 方程两边对x求导, 0 d d d d x y e e x y y x x y 解得 , d d y x x e e y x y x 0代入原方程 y 0, 0 0 0 d d y y x x x x e e y x y 1