
第四章中值定理与导数的应用习题课主要内容典型例题高等数学(上册)
主要内容 典型例题 第四章 中值定理与导数的应用 习 题 课
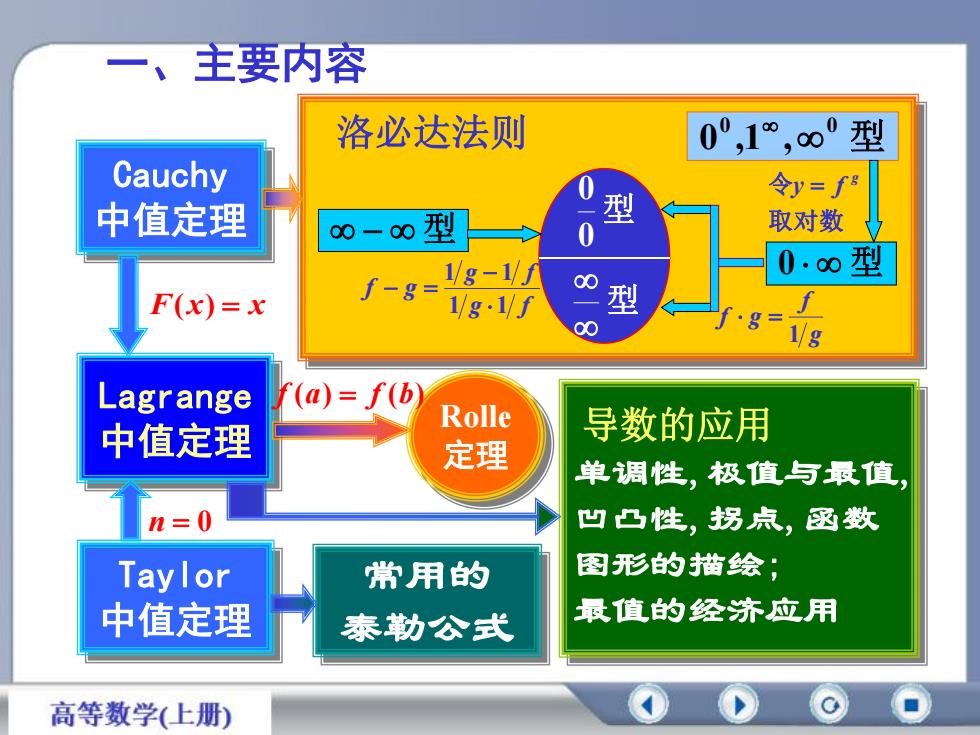
一、主要内容洛必达法则0°,1°,80°型Cauchy令y=f80型-0中值定理取对数8-8型0.8型I-8 -V8型F(x)= xf·g81/9r(a)= f(bLagrangeRolle导数的应用中值定理定理单调性,极值与最值凹凸性,拐点,函数n=0图形的描绘;Taylor常用的最值的经济应用中值定理泰勒公式高等数学(上册)
洛必达法则 Rolle 定理 Lagrange 中值定理 常用的 泰勒公式 0 0 ,1 , 0 型 型 0 型 型 0 0 型 Cauchy 中值定理 Taylor 中值定理 F(x) x f (a) f (b) n 0 g f f g 1 g f g f f g 1 1 1 1 取对数 令 g y f 单调性,极值与最值, 凹凸性,拐点,函数 图形的描绘; 最值的经济应用 导数的应用 一、主要内容

习题课第三章微分中值定理与导数的应用1.微分中值定理及其相互关系f(a)= f(b)拉格朗门中值定理罗尔定理f(b)- f(a)f()= 0F'(5)= sb-aF(x)= xF(x)= xn=0f(a) = f(b)柯西中值定理泰勒中值定理f(b)-f(a) - f'()f(x)= f(xo)+ f'(xo)(x - xo)F(b)-F(a)F'(é)(n)(x)(x - x0)"'(E)(x -x0)n+1+(n+l)高等数学(上册)
3 f (a) f (b) 1.微分中值定理及其相互关系 罗尔定理 f ( ) 0 ( ) ( ) ( ) ( ) ( ) ( ) F f F b F a f b f a 拉格朗日中值定理 ( ) ( ) ( ) f a f b F x x 1 0 ( 1)( )( ) ( 1)! 1 n n f x x n 柯西中值定理 F(x) x 泰勒中值定理 n n f x x x n ( )( ) ! 1 0 0 ( ) 第三章 微分中值定理与导数的应用 习题课 b a f b f a f ( ) ( ) ( ) ( ) ( ) ( )( ) 0 0 0 f x f x f x x x n 0

1.罗尔中值定理罗尔(Rolle)定理如果函数f(x)在闭区间[a,bl上连续,在开区间(a,b)内可导,且在区间端点的函数值相等,即f(a)=f(b),那末在(a,b)内至少有一点(a<E<b),使得函数f(x)在该点的导数等于零即f()=0高等数学(上册)
1. 罗尔中值定理 罗尔(Rolle)定理 如果函数f (x)在闭区间 [a,b]上连续,在开区间(a,b)内可导,且在区间端 点的函数值相等,即 f (a) f (b),那末在(a,b) 内至少有一点(a b),使得函数f (x)在该 点的导数等于零, 即 ( ) 0 ' f

2.拉格朗日中值定理拉格朗日(Lagrange)中值定理如果函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,那未在(a,b)内至少有一点(a<<b),使等式f(b)- f(a)= f ()(b-a) 成立有限增量公式(0 <0 <1)Ay = f'(x, + x).Ax增量△y的精确表达式高等数学(上册)
2. 拉格朗日中值定理 拉格朗日(Lagrange)中值定理 如果函数f (x) 在闭区间[a,b]上连续,在开区间(a,b)内可导,那 末在(a,b)内至少有一点(a b),使等式 ( ) ( ) ( )( ) ' f b f a f b a 成立. ( ) (0 1). y f x0 x x 增量y的精确表达式. 有限增量公式