
第八节闭区间上连续函数的性质最大值最小值定理与有界性「i零点定理与介值定理三、小结思考题高等数学(上册)
一 、最大值最小值定理与有界性 二、零点定理与介值定理 三、小结 思考题 第八节 闭区间上连续 函数的性质

一、最大值和最小值定理与有界性定义:对于在区间I上有定义的函数,f(x)如果有 xεI,使得对于任一xEI都有f(x)≤ f(x)(f(x) ≥ f(xo))则称f(x)是函数f(x)在区间I上的最大(小)值例如,J=1 + sinx,,在[0,2元]上,ymax =2, Jmin = 0;y=sgnx,在(-o0,+o0)上, max =1, ymin = -1;当x>0?当x=0在(0,+o0)上,Jmax = ymin = 1.0y=sgnx=3当x<0-1高等数学(上册)
一、最大值和最小值定理与有界性 定义: 0 0 0 0 ( ) ( ) ( ), , ( ( ) ( )) ( ) ( ) ( ) . I f x x I x I f x f f x f x f x f x I x 对于在区间 上有定义的函数 如果有 使得对于任一 都有 则称 是函数 在区间 上的最大 小 值 例如, y sgnx,在(,)上, 2, ymax 1; ymin 在(0,)上, 1. ymax ymin y 1 sin x, 在[0,2]上, 0; ymin 1, ymax 1 0 0 0 1 0 sgn x x x y x 当 当 当
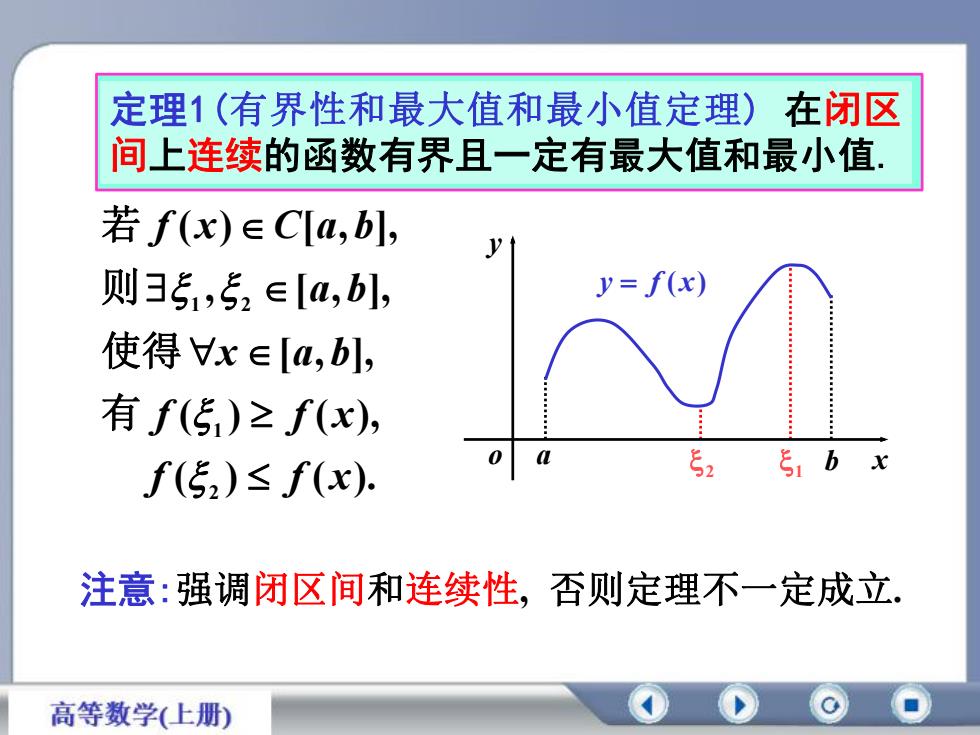
在闭区定理1(有界性和最大值和最小值定理)间上连续的函数有界且一定有最大值和最小值若 f(x) E C[a,b],Jy= f(x)则3,5, E[a,b],使得Vx E[a,b],有 f(S)≥ f(x),aS051bxf(52)≤ f(x)注意:强调闭区间和连续性,否则定理不一定成立高等数学(上册)
定理1(有界性和最大值和最小值定理) 在闭区 间上连续的函数有界且一定有最大值和最小值. a 2 1 b x y o y f ( x) ( ) ( ). ( ) ( ), [ , ], , [ , ], ( ) [ , ], 2 1 1 2 f f x f f x x a b a b f x C a b 有 使得 则 若 注意:强调闭区间和连续性, 否则定理不一定成立
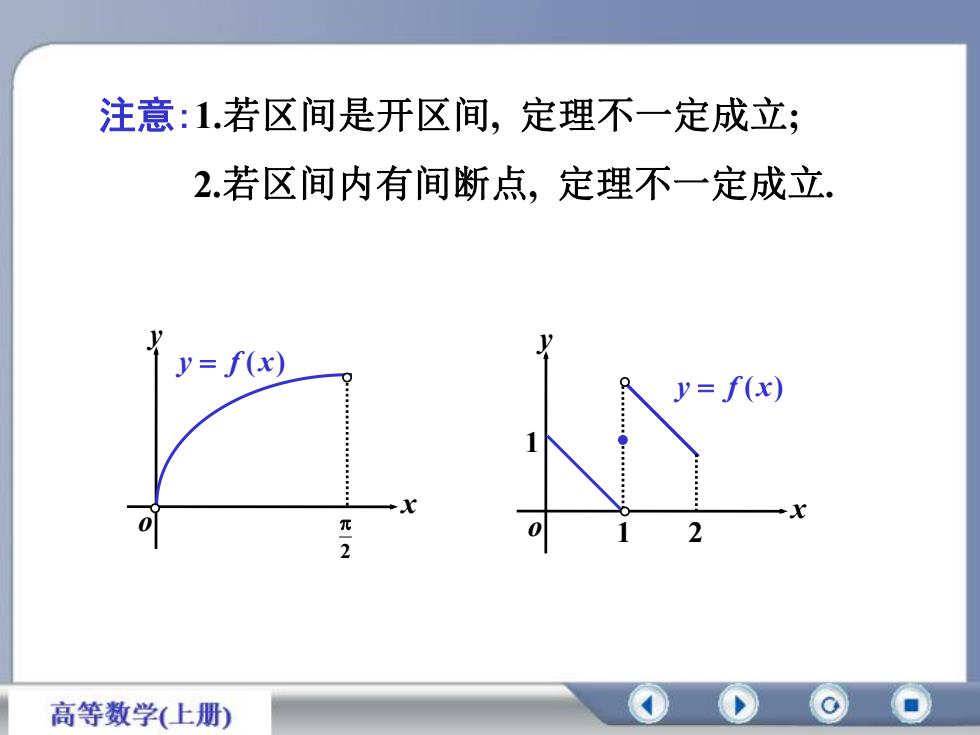
注意:1.若区间是开区间,定理不一定成立;2.若区间内有间断点,定理不一定成立y= f(x)y= f(x)...................xx0元0212高等数学(上册)
x y o y f ( x) 1 2 1 x y o 2 y f ( x) 注意:1.若区间是开区间, 定理不一定成立; 2.若区间内有间断点, 定理不一定成立

二、零点定理与介值定理定义:1如果 x使 f(x)=0,则 x。称为函数f(x)的零点.a,b设函数f(x)在闭区间定理2(零点定理)上连续,且f(a)与f(b)异号(即f(a)·f(b)<0那么在开区间(a,b)内至少有函数f(x)的一个零点,即至少有一点(a<<b),使f()=0.即方程f(x)=0在(a,b)内至少存在一个实根:高等数学(上册)
二、零点定理与介值定理 定义: ( ) . ( ) 0 , 0 0 0 的零点 如果 使 则 称为函数 f x x f x x 即方程 f (x) 0在(a,b)内至少存在一个实根