
第三节导数的应用曲线的凹凸性与拐点小结思考题高等数学(上册)
第三节 导数的应用 曲线的凹凸性与拐点 小结 思考题
一、曲线凹凸性的判别法(concave and convex)1.定义如何研究曲线的弯曲方向VBox高等数学(上册)
(concave and convex) 一、曲线凹凸性的判别法 1.定义 如何研究曲线的弯曲方向 x y O A B C
yy=f(x)Vy= f(x)X,+x,XXxfXi+X2X2 xx,22图形上任意弧段图形上任意弧段位于所张弦的上方位于所张弦的下方定义1 设f(x)eC[a,b],如果对(a,b)内任意两点Xi,X2,恒有f(x)+ f(x2)f(x)+ f(x)Xi+xf(±i +x22222那么称f(x)在(a,b)内的图形是凹(凸)的高等数学(上册)
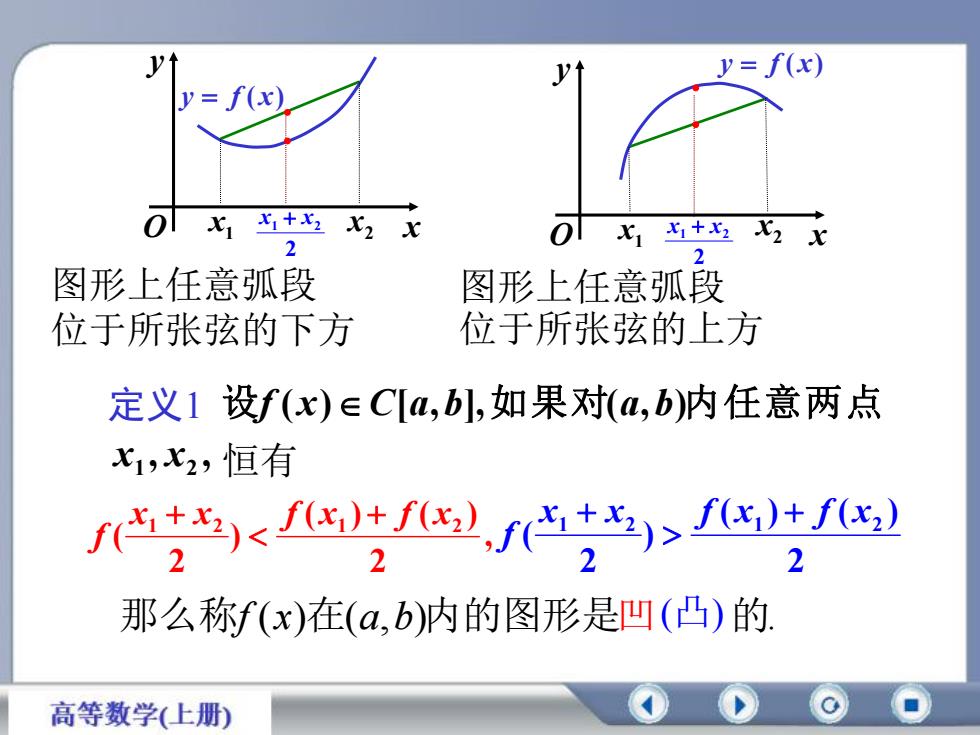
y f ( x) y f ( x) x1 2 x 1 x x2 定义1 设f (x)C[a,b],如果对(a,b)内任意两点 , 2 ( ) ( ) ) 2 ( 1 2 1 2 x x f x f x f , , x1 x2 恒有 那么称f (x)在(a,b)内的图形是凹 的. 2 ( ) ( ) ) 2 ( 1 2 1 2 x x f x f x f (凸) 2 x1 x2 2 x1 x2 图形上任意弧段 位于所张弦的下方 图形上任意弧段 位于所张弦的上方 x y O x y O
X=f(x)Vy=f(x)txx曲线弧上每一点的切线都在曲线的下(上)定义2方,称为凹(凸)弧丛几何直观上,随着x的增大,凹弧的曲线段f(x)的切线斜率是单增的,即f'(x)是单增的,而凸弧的切线斜率是单减的,即f(x)是单减的.利用二阶导数判断曲线的凹凸性高等数学(上册)
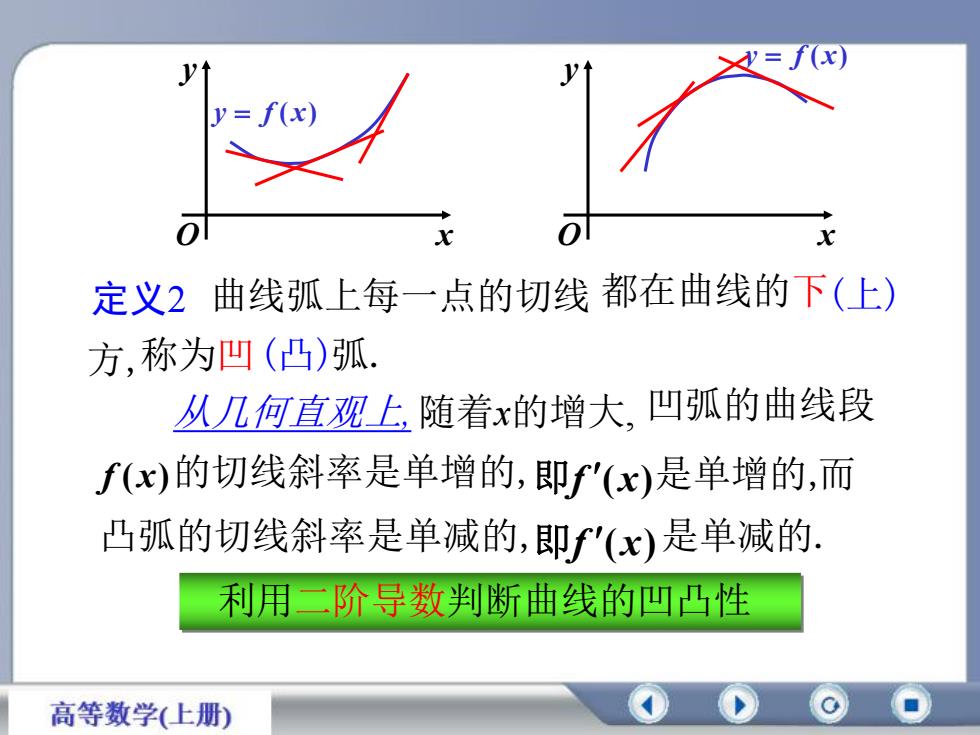
y f ( x) y f ( x) 定义2 曲线弧上每一点的切线 (上) 方,称为凹(凸)弧. 凹弧的曲线段 f (x)的切线斜率是单增的,即f (x)是单增的, 凸弧的切线斜率是单减的,即f (x)是单减的.而 利用二阶导数判断曲线的凹凸性 从几何直观上, 随着x的增大, 都在曲线的下 x y O x y O
2.凹凸性的判别法VBBy= f(x)y= f(x)Aobaolb xaxf'(x) 递减 f"(x)<0f'(x) 递增 f"(x)>0定理2如果f(x)在[a,b]上连续,在(a,b)内具有二阶导数,在(a,b)内,若f"(x)>0 (<0),则f(x)在[a,b]上的图形是凹(凸)的.高等数学(上册)
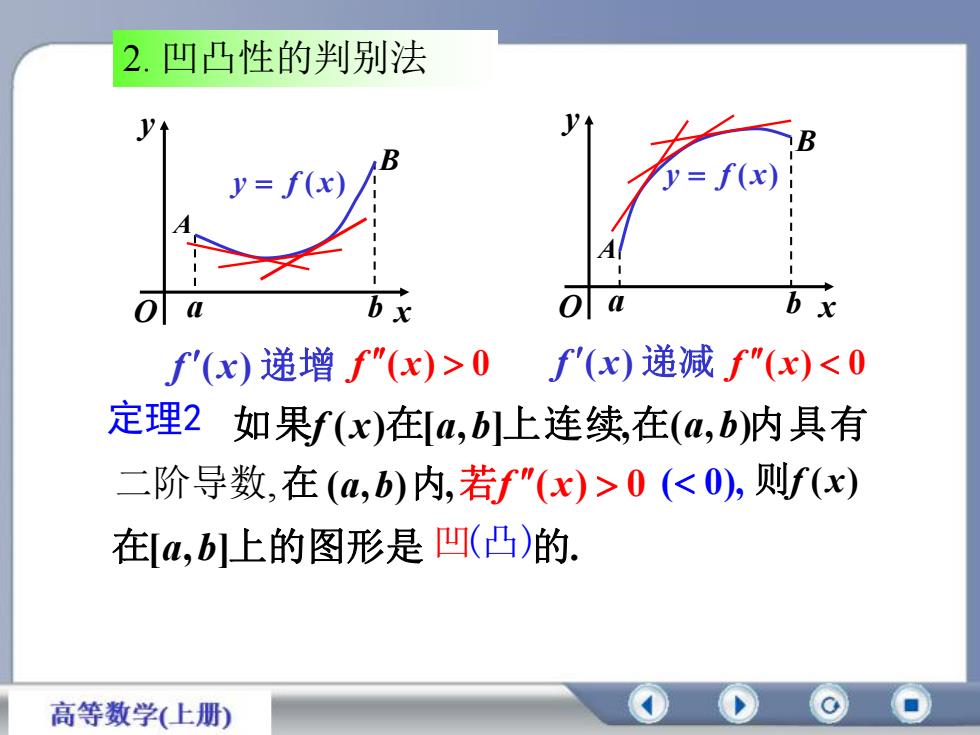
f (x) 递增 f (x) 0 f (x) 递减 f (x) 0 定理2 如果f (x)在[a,b]上连续,在(a,b)内具有 二阶导数,在 (a,b)内,若f (x) 0 ( 0), 则f (x) 在[a,b]上的图形是 凹(凸)的. 2. 凹凸性的判别法 x y O a b A B y f ( x) x y O a b A B y f ( x)