《高等数学》课程教学资源（PPT课件）第十章 重积分 10-02 第二节 二重积分的计算法

例 5 求[[xe-dxdy,其中 D 是以(0,0),(1,1),D(0,1)为顶点的三角形分析此题方法同例4.但要注意[e-"dy无法用初等函数表示，0.80.60.4所以积分时必须考虑积分顺序0.20.20.40.60.8Jf x'e-"dxdy = f'dyf'xe-"dxD(1-=)=二1,21

例 5 求 − D y x e dxdy 2 2 ，其中 D 是以(0,0),(1,1), (0,1)为顶点的三角形. 2 y e dy −  无法用初等函数表示， 2 2 y D x e dxdy −  1 2 2 0 0 y y dy x e dx − =   2 3 1 0 3 y y e dy − =   2 2 1 2 0 6 y y e dy − =   1 2 (1 ). 6 e = − 所以积分时必须考虑积分顺序. 分析 此题方法同例4. 但要注意

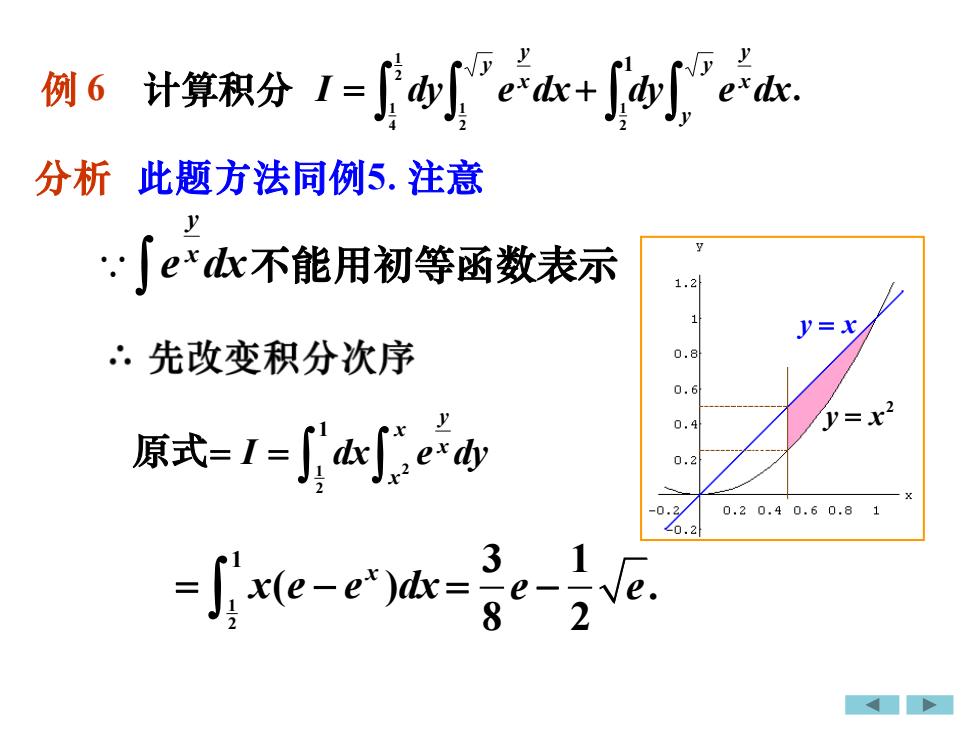
例 6计算积分exdx分析此题方法同例5.注意2ye~dx不能用初等函数表示1.21y=x0.8：先改变积分次序0.6J=x?0.4dx原式=I=exd0.20.20.40.60.80120.23Odx=xleP822

例 6 计算积分   = y x y I dy e dx 2 1 2 1 4 1   + y y x y dy e dx 1 2 1 .  e dx x y  不能用初等函数表示 原式 1 2 2 1 y x x x = = I dx e dy   1 2 1 ( ) x = − x e e dx  3 1 . 8 2 = −e e 2 y = x y = x 分析 此题方法同例5. 注意

例7求两个底圆半径为R的直角圆柱面所围的体积1z分析此题注意利用二重积分的几何意义IR x+ y?=R2解设两个直圆柱方程为x?+ y?= R, x? +z?= R利用对称性,考虑第一卦限部分， +z= R?其曲顶柱体的顶为=R?-x

x y z R o R 设两个直圆柱方程为 2 2 2 xyR + = , 利用对称性,考虑第一卦限部分, 其曲顶柱体的顶为 2 2 2 x z R + = 2 2 z R x = − 分析 此题注意利用二重积分 的几何意义. 例 7 求两个底圆半径为R 的直角圆柱面所围的体积. 解

z= R2-x2顶为1z0≤y≤/r2-x?(x,y)eD:R x+ y? =R?0≤x≤R则所求体积为AR-yV=8J], VR2-x dxd yx? +z= R?VR?-x=8[^R?-x dxdy-16R3:88(R?-x")dx =-3

x y z R o R 顶为 则所求体积为 2 2 0 d R x y −  2 2 0 8 ( )d R = − R x x  16 3 3 = R 2 2 z R x = − 2 2 0 ( , ) : 0 y R x x y D x R    −      2 2 0 8 d R = − R x x 

二、利用极坐标系计算二重积分A, =(r, +Ar) . A0, -△60=0. +40r=r+Ar(2r + Ar,)A, A0.r=r;Ao;i+(r,+ r) Ar A0,20= 0,=r,·Ar ·Ae,A0JJ f(x, y)dxdy = J f(rcos0,rsin)rdrde.DD

A o D  i i r r = i i r r r = +     = +  i i   = i 1 1 2 2 ( ) 2 2 i i i i i i  = +    −      r r r 1 (2 ) 2 i i i i = +     r r r  ( ) 2 i i i i i r r r r  + +  =    , i i i =     r r  ( , ) ( cos , sin ) . D D f x y dxdy f r r rdrd =      二、利用极坐标系计算二重积分