
第二节对坐标的曲线积分对坐标的曲线积分的概念与性质对坐标的曲线积分的计算法两类曲线积分之间的联系小结思考题
第二节 对坐标的曲线积分 ◼ 对坐标的曲线积分的概念与性质 ◼ 对坐标的曲线积分的计算法 ◼ 两类曲线积分之间的联系 ◼ 小结 思考题
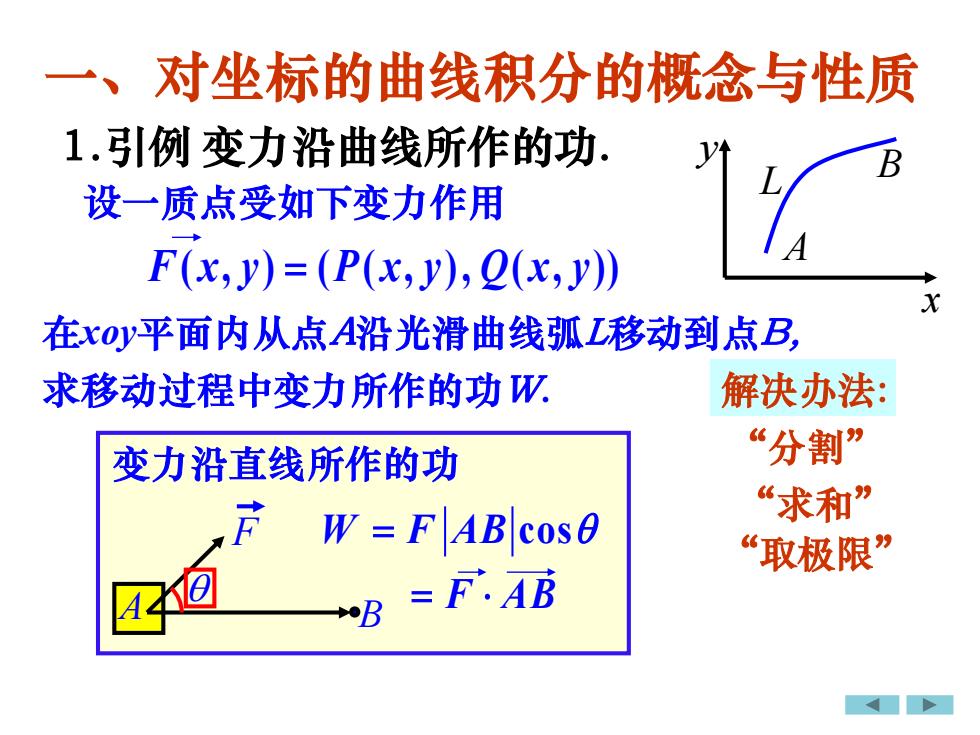
一、对坐标的曲线积分的概念与性质1.引例变力沿曲线所作的功VBL设一质点受如下变力作用AF(x, y)=(P(x,y),Q(x,y)x在xov平面内从点A沿光滑曲线弧L移动到点B求移动过程中变力所作的功W解决办法:“分割”变力沿直线所作的功“求和”FW = F|ABcosa“取极限”白= F.ABA4B
一、对坐标的曲线积分的概念与性质 1.引例 变力沿曲线所作的功. 设一质点受如下变力作用 在xoy平面内从点A沿光滑曲线弧L移动到点B, A B L x y W F AB = cos “分割” “求和” “取极限” 变力沿直线所作的功 求移动过程中变力所作的功W. 解决办法: A = F AB B F F x y P x y Q x y ( , ) ( ( , ), ( , )) =

1)“分割”把L分成n个小弧段,F沿Mk-MF(5k,nk)y为△Wk,则所做的功为B1Ayk12W=AWAxkkk=1A2)“求和”x用有向线段Mk-M =(Axk,Ayk)M-M有向小弧段在Mk-iM,上任取一点近似代替,(k,nk),则有AW,~ F(5k,nk).Mk-M= P(5k,nk)Ax, +Q(5k,nk)Ayk
M k −1 Mk A B x y 1) “分割”. 2) “求和” L 把L分成n个小弧段, 有向小弧段 近似代替, 则有 k k ( , ) ( , ) P x Q y k k k k = + 所做的功为 F 沿 k 1 ( , ) W F M M k k k k − ( , ) F k k 1 n k k W W = = 则 用有向线段 在 上任取一点 k y k x

Z [ P(5,nk)Axe +Q(Sk, nk)Aye ]W~k=13)“取极限”Z[P(5h, nk)4x, +Q(5h, nk)4yk]W = lim→0k=1F(5k,nk)(其中为 n个小弧段的VB最大长度)1DykAxkx
3) “取极限” 1 n k W = P x Q ( , ) ( , ) k k k k k k + ξ y 0 1 lim n k W → = = ( , , P k k k k k k ξ η )Δx Q( + ξ η )Δy M k −1 L Mk A B x y ( , ) F k k k y k x (其中 为 n 个小弧段的 最大长度)

2.定义.设L为xoy平面内从A到B的一条有向光滑弧,在L上定义了一个向量函数F(x,y)=(P(x,y),Q(x,y)若对L的任意分割和在局部弧段上任意取点n极限Z[1limP(5k,nk)Ax,+Q(5k,nk)Ayk→0k=1记作P(x,y)dx +Q(x,y)dy都存在
2.定义. 设L为xoy平面内从A到B的一条有向光滑 弧, 若对L的任意分割和在局部弧段上任意取点, ( , )d ( , )d 都存在, L P x y x Q x y y + ( , ) P x k k k ( , ) Q y k k k + 1 n k= lim →0 在L上定义了一个向量函数 极限 记作