
dx[~ f(x,y)dy的次序.例1改变积分分析交换积分次序的步骤:(1)将已给的二次积分的积分限得出相应的二重积分的积分区域,(2)按相反顺序写出相应的二次积分解:由积分的上下限知0.80≤x≤1y=1-x0.6D:[0≤y≤1-x0.20.40.60.8积分区域如图J,dyf," f(x, y)dx.原式=
y x = −1 例 1 改变积分 1 1 0 0 ( , ) x dx f x y dy − 的次序. 原式 1 1 0 0 ( , ) y dy f x y dx − = . 解: 积分区域如图 分析 交换积分次序的步骤:(1) 将已给的二次积分 的积分限得出相应的二重积分的积分区域, (2) 按相 反顺序写出相应的二次积分. 由积分的上下限知 0 1 : 0 1 x D y x −
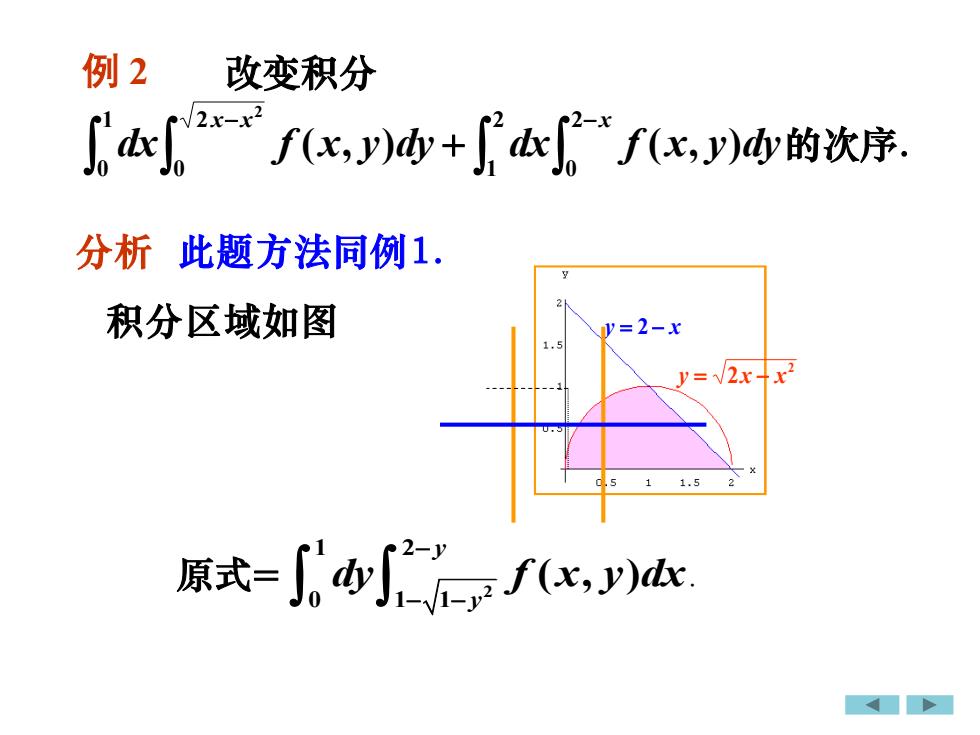
例 2改变积分2x-xdxf(x,y)dy的次序dxf(x, y)dy +J0分析此题方法同例1.积分区域如图V=2-x1.5V= /2x+x21.5原式=f(x, y)dx
y = 2 − x 2 y = 2x − x 例 2 改变积分 − − + x x x dx f x y dy dx f x y dy 2 0 2 1 2 0 1 0 ( , ) ( , ) 2 的次序. 原式 2 1 2 0 1 1 ( , ) y y dy f x y dx − − − = . 分析 此题方法同例1. 积分区域如图
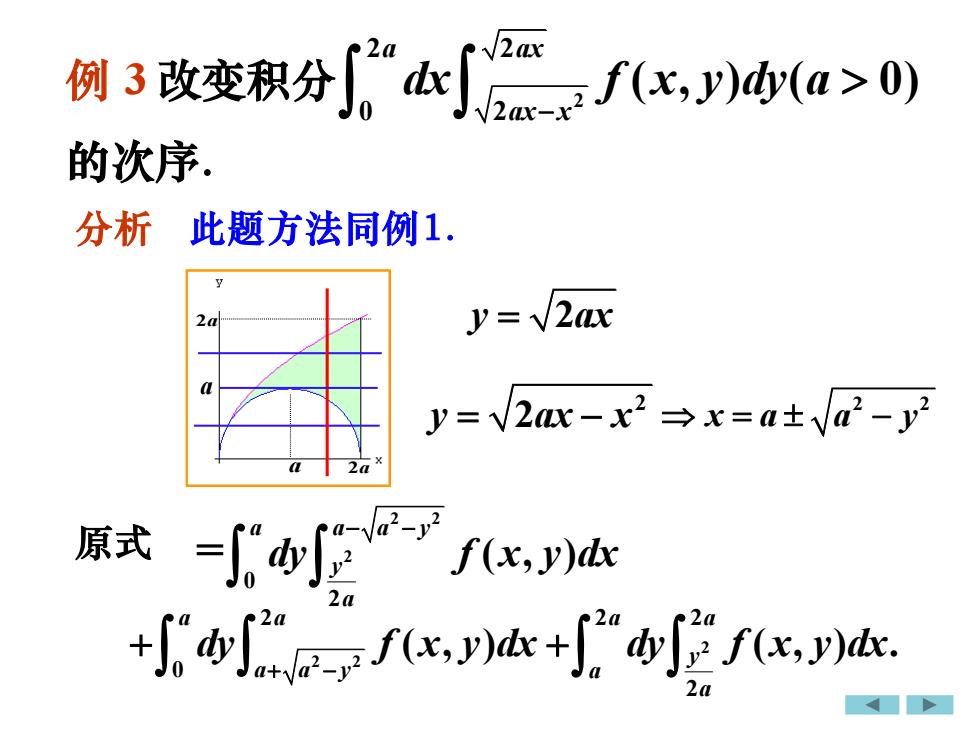
2a20例3改变积分dxf(x, y)dy(a > 0)的次序。分析此题方法同例1.y = V2axy=~2ax-x2 →x=a±ya-y原式f(x, y)dx2aI"dy/z f(x, y)dx.,y)dx +f(x,2a
例 3 改变积分 2 2 2 0 2 ( , ) ( 0) a ax ax x dx f x y dy a − 的次序. y ax = 2 分析 此题方法同例1. = 2 2 2 0 2 ( , ) a a a y y a dy f x y dx − − 原式 2 2 2 0 ( , ) a a a a y dy f x y dx + − + 2 2 2 2 ( , ) . a a y a a + dy f x y dx 2 y ax x = − 2 2 2 = − x a a y a 2a 2a a
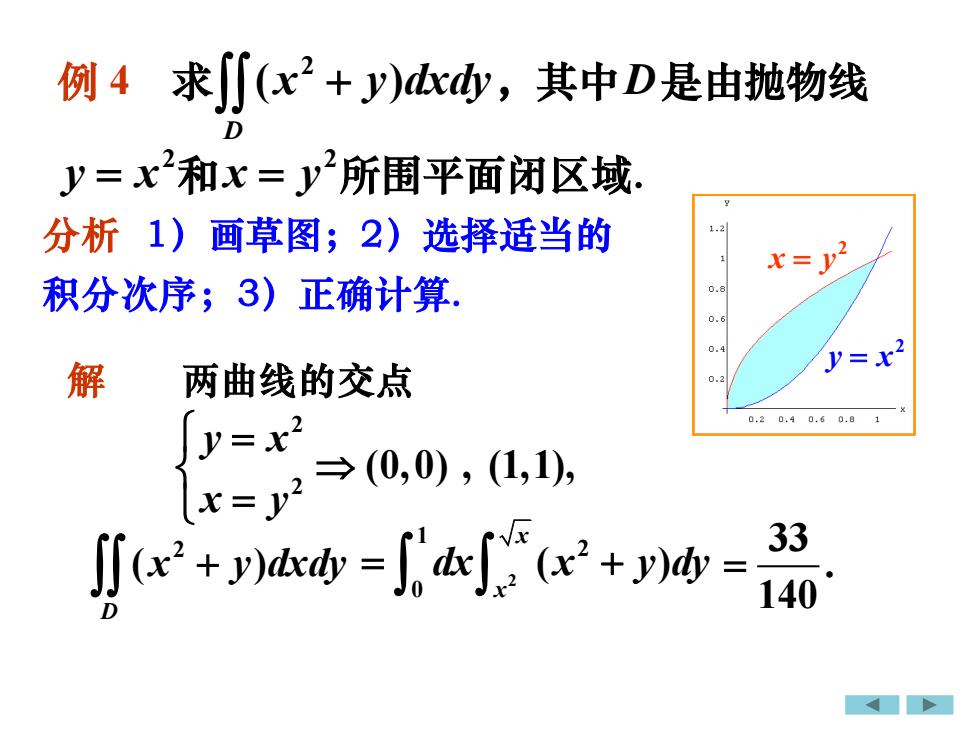
求[J(x2+y)dxdy,其中D是由抛物线例4D=2和x=所围平面闭区域分析 1)亚画草图;2)选择适当的X=积分次序;3)正确计算0.0.y=x?解两曲线的交点0.2.0.40.60.8-=→ (0,0) , (1,1)33 dx/ (x? +[ (x? + y)dxdyVa140D
例 4 求 + D (x y)dxdy 2 ,其中D是由抛物线 2 y = x 和 2 x = y 所围平面闭区域. 解 2 2 (0,0) , (1,1), y x x y = = 2 ( ) D x y dxdy + 2 1 2 0 ( ) x x = + dx x y dy 33 . 140 = 2 y = x 2 x = y 2 y = x 2 x = y 两曲线的交点 分析 1)画草图;2)选择适当的 积分次序;3)正确计算

计算二重积分时,恰当的选取积分次序十分重要,它不仅涉及到计算繁简问题,文涉及到能否进行计算的问题凡遇如下形式积分:sinddx,{sinx'dx,[cosx'dx,Xax"dx, fe'dx, J x,o等等,一定要放在nx后面积分
计算二重积分时,恰当的选取积分次序十分重要, 它不仅涉及到计算繁简问题,又涉及到能否进行 计算的问题. 凡遇如下形式积分: d , sin x x x d , 2 e x x , ln d x x 等等, 一定要放在 后面积分. sin d , 2 x x cos d , 2 x x d , 2 e x x − e dx, x y