《高等数学》课程教学资源（PPT课件）第十一章 曲线曲面积分 11-06 第六节 高斯公式、通量与散度

第六节高斯公式通量与散度高斯公式■简单的应用物理意义一通量与散度函数小结思考题

第六节 高斯公式 通量与散度 ◼ 高斯公式 ◼ 简单的应用 ◼ 物理意义—通量与散度 ◼ 函数 ◼ 小结 思考题

高斯(Gauss)公式定理1设空间闭区域2由分片光滑的闭曲面乙所围成，乙的方向取外侧，函数P,Q,R在则有2上有连续的一阶偏导数，aRapa0Jdxdydz+SDF.CaxOzay=$f, Pd ydz+Qdzdx+ Rdxd y（Gauss公式）

一、高斯(Gauss)公式 定理1 设空间闭区域由分片光滑的闭曲 上有连续的一阶偏导数, d d d d d d P y z Q z x R x y  = + +  面所围成,的方向取外侧, 函数P, Q, R在 则有 (Gauss公式)

aR下面先证：J.2$f, Rdxdydxdydz=N证明设Q:z,(x,y)<z(x,y)≤zz(x, y), (x,y)eDx为XY型区域Z=Z,UZ,UE3,(取下侧)Z, : z = z,(x, y),E, : z = z2(x,y),(取上侧)匕，：母线平行于z轴的柱面(取外侧)则

d d d R x y z  z    d d R x y  =  下面先证: 证明 设 1 2 3 为XY型区域,  =    , 1 1  = : ( , ), z z x y 2 2  = : ( , ), z z x y 3  : 母线平行于z轴的柱面. (取外侧) (取下侧) (取上侧) 则

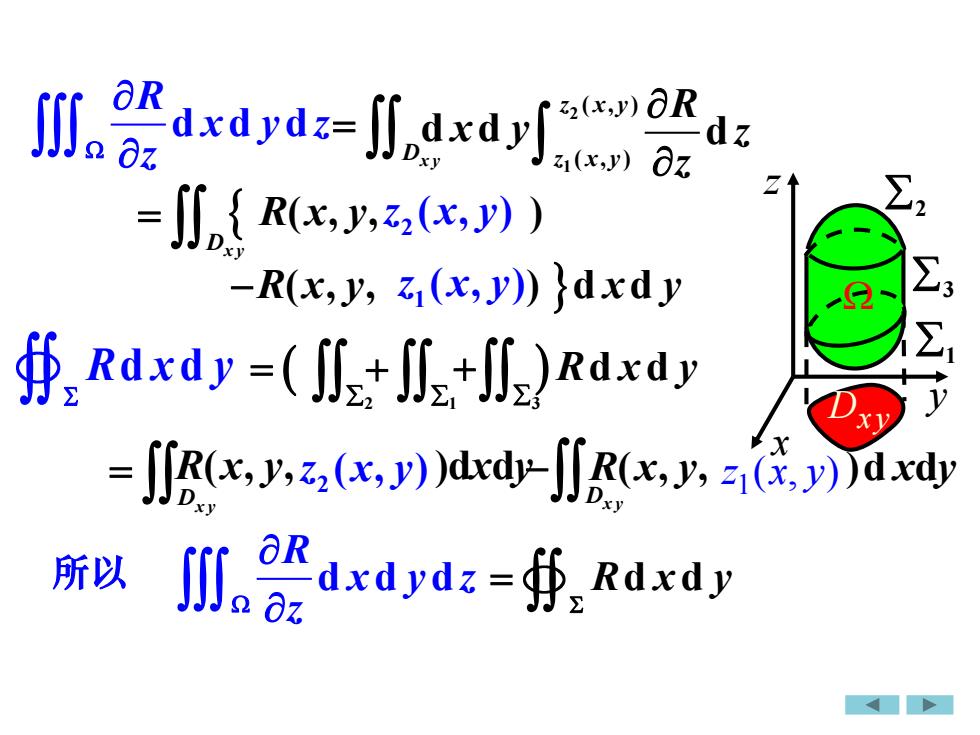
aRz(x,y) ORI.2dxdydz=dxdjdzDxyOzz(x,y)Z1ZJJD( R(x,y,z2(x, ) )Z3-R(x,y, zi(x,y) /dxd y2Z折,Rdxdy =( JJ,+ J,+J2)Rdxdy>yDxy[IR(x, y,z,(x, y))dxdyR(x, y, zi(x, y))d xdyDaRI所以dxdydz=f, Rdxdy2 Oz.-

2 3 1  z y x Dxy  R x y ( , , ) −R x y x y ( , , ) d d  2 1 ( , ) ( , ) d z x y z x y R z z    Dx y =  2 z x y ( , ) 1 z x y ( , ) d d R x y   Dx y =  ( 2 =  d d d R x y z  z    d dx y 1 +  3 + ) R x y d d R x y x y ( , , )d d Dx y − Dx y =  2 z x y ( , ) R x y x y ( , , )d d ( , ) 1 z x y 所以 d d d R x y z  z    d d R x y  = 

则可引进辅助面若Q不是XY-型区域将其分割成若干个XY-型区域在辅助面正反两侧面积分正负抵消故上式仍成立apJIdxdydz =$, Pd ydz类似可证oxQ0.%dxdydz = $f,Qdzdx三式相加，即得所证Gauss公式：aRaodp(%xdxd ydzazaxay-$f,Pd ydz+Qdzdx+ Rdxdy>

若不是XY–型区域, 则可引进辅助面 将其分割成若干个XY–型区域, 故上式仍成立. 在辅助面 正反两侧面积分正负抵消, 类似可证 d d d Q x y z  y    d d d d d d P y z Q z x R x y  = + +  ( )d d d P Q R x y z x y z   + +     d d Q z x  =  d d d P x y z  x    d d P y z  =  三式相加, 即得所证Gauss公式：