
第二节二重积分的计算法■利用直角坐标计算二重积分利用极坐标计算二重积分二重积分的换元法■小结思考题
◼ 利用直角坐标计算二重积分 ◼ 利用极坐标计算二重积分 ◼ 二重积分的换元法 ◼ 小结 思考题 第二节 二重积分的计算法
利用直角坐标系计算二重积分一、如果积分区域为:a≤x≤b,P (x)≤ y≤P(x)[X一型]yy=Φ2(x)y=P2(x)DDy=Φ(x)y=pi(x)ah11其中函数Pi(x)P2(x)在区间[a,b]上连续
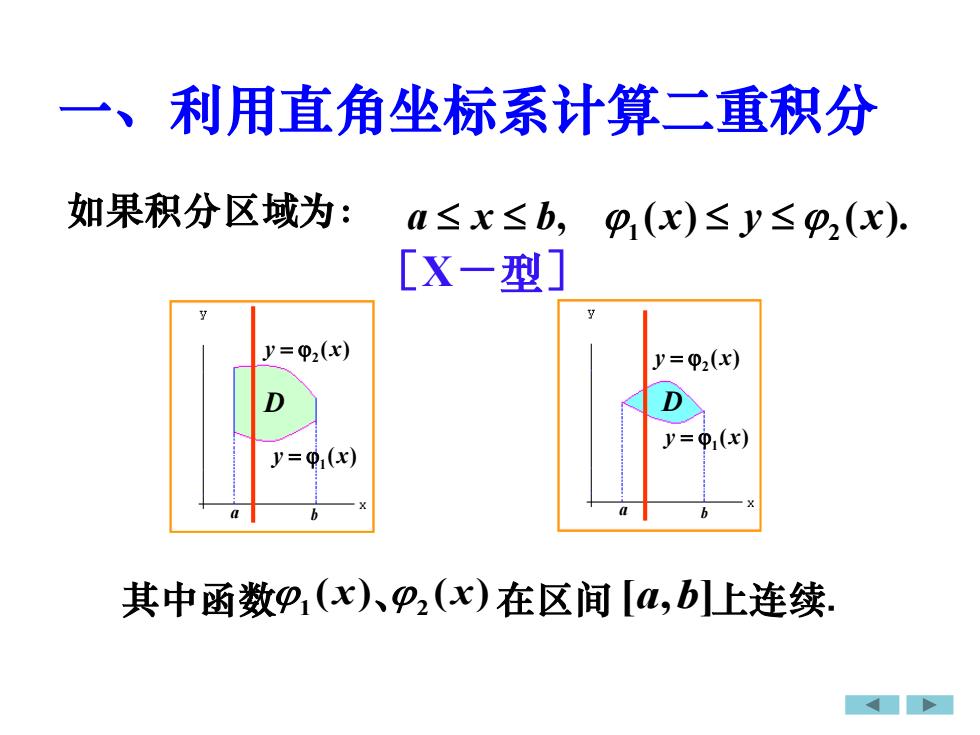
如果积分区域为: a x b , 1 2 ( ) ( ). x y x 其中函数 1 ( ) x 、 2 ( ) x 在区间 [ , ] a b 上连续. 一、利用直角坐标系计算二重积分 [X-型] ( ) 2 y = x a b D ( ) 1 y = x D a b ( ) 2 y = x ( ) 1 y = x
:f(x,J)d 的值等于以D为底,以曲面Dz=f(x,y)为曲顶柱体的体积。z =f(x,y)7.4应用计算“平行截面面积为已知的立体求A(x)体积”的方法,y=Φ2(x)+XDdXKy= Pi(x)P2(x)SJ f(x,y)do = J"得dxf (x, y)dy.(x)D
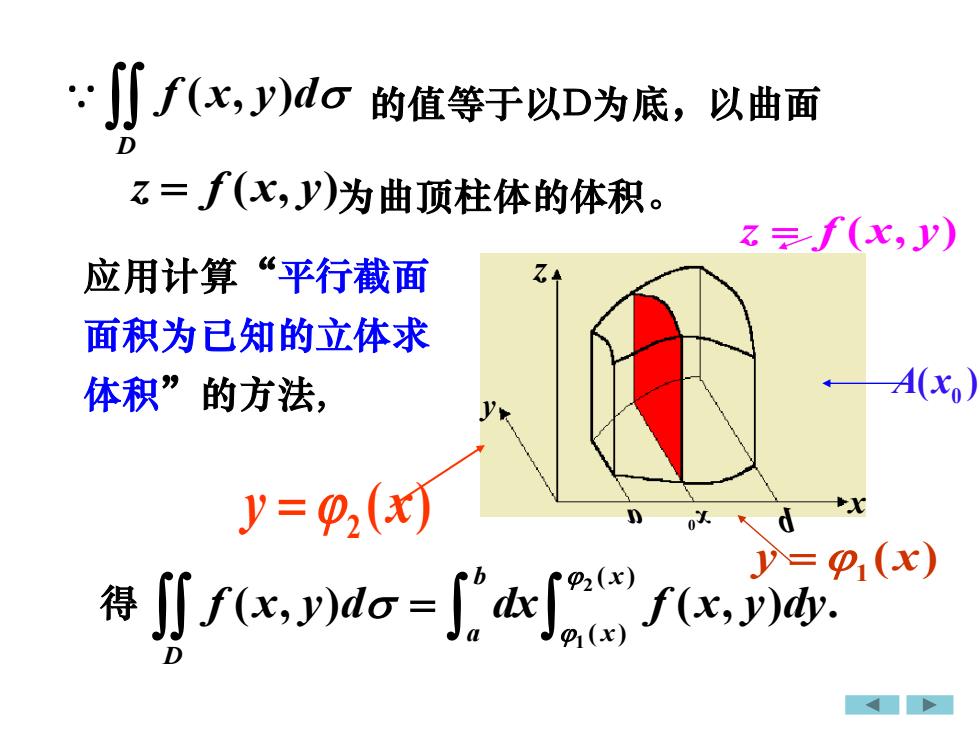
应用计算“平行截面 面积为已知的立体求 体积”的方法, a 0 x b z y x 0 A x( ) z f x y = ( , ) 1 y x = ( ) 2 y x = ( ) 2 1 ( ) ( ) ( , ) ( , ) . b x a x D f x y d dx f x y dy = 得 ( , ) D f x y d z f x y = ( , ) 的值等于以D为底,以曲面 为曲顶柱体的体积

如果积分区域为:c≤≤d,(y)≤x≤2(y)[Y-型]yPl(y)x=x =0.()DDx=9P,(y)x =Φ2 (y)P2(y)J f(x,y)do =f(x,y)dx.P(y)D
( , ) ( , ) . ( ) ( ) 2 1 = D d c y y f x y d dy f x y dx 如果积分区域为: c y d , 1 2 ( ) ( ). y x y [Y-型] 2 x y = ( ) 1 x y = ( ) D c d c d 2 x y = ( ) 1 x y = ( ) D
X型区域的特点:穿过区域耳平行于轴的直线与区域边界相交不多于两个交点Y型区域的特点:穿过区域且平行于x轴的直线与区域边界相交不多于两个交点,若区域如图,则必须分割。在分割后的三个区域上分别使用积分公式 = + + .DDLD2D3
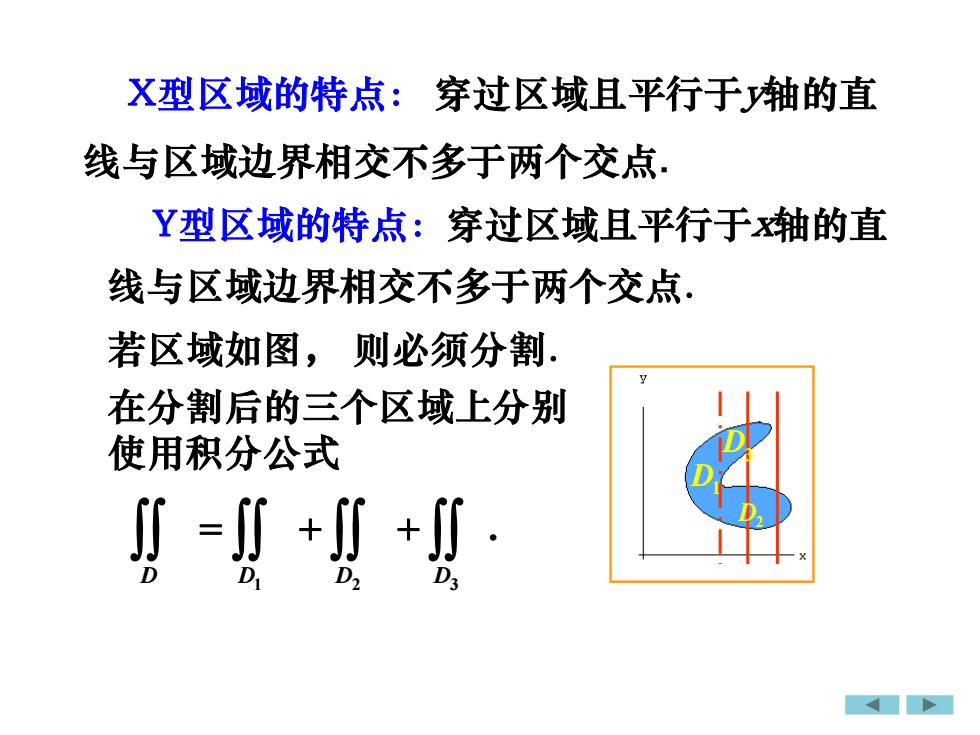
X型区域的特点: 穿过区域且平行于y轴的直 线与区域边界相交不多于两个交点. Y型区域的特点:穿过区域且平行于x轴的直 线与区域边界相交不多于两个交点. 若区域如图, D3 D2 D1 在分割后的三个区域上分别 使用积分公式 1 2 3 . D D D D = + + 则必须分割