
第四节对面积的曲面积分surface integral概念的引入对面积的曲面积分的定义对面积的曲面积分的计算法小结
第四节 对面积的曲面积分 surface integral 概念的引入 对面积的曲面积分的定义 对面积的曲面积分的计算法 小结

对面积的曲面积分一、概念的引入实例若曲面光滑的,它的面密度为连续函数u(x,y,z),求它的质量所谓曲面光滑解第一步:将Z分为许即曲面上各点处都以ds为代表,取(x,y,2有切平面,且当点在曲面上连续移动时dS的质量为:AM ~ d切平面也连续转动第二步:求和取极限M = J u(x,y,z)dsZ
实例 解 第一步: 将Σ分为许多极其微小的子域, 以dS为代表, dS的质量为: M dM 第二步: 求和取极限 = M ( x, y,z)dS 则 = (x, y,z)dS 取 (x, y,z)dS, 所谓曲面光滑 即曲面上各点处都 有切平面,且当点在 曲面上连续移动时, 切平面也连续转动. 若曲面是 光滑的,它的面密度为连续函数 (x, y,z), 求它的质量. 对面积的曲面积分 一、概念的引入
对面积的曲面积分7z(x,D74S.(5i,ni,s.)二、对面积的曲面1.定义+7Dxy设曲面是光滑的,函(5,ni,)1有界.把Z任意分成n小块S(ZS,同时也表示②设点(5;,n,5,)为4S,上第i小块曲面的面积)3并作和任意取定的点,作乘积f(i,ni,S,)AS,nXZf(5,ni,5i)4S;如果当各小块曲面的直径i=1的最大值 →0时,这和式的极限存在,则
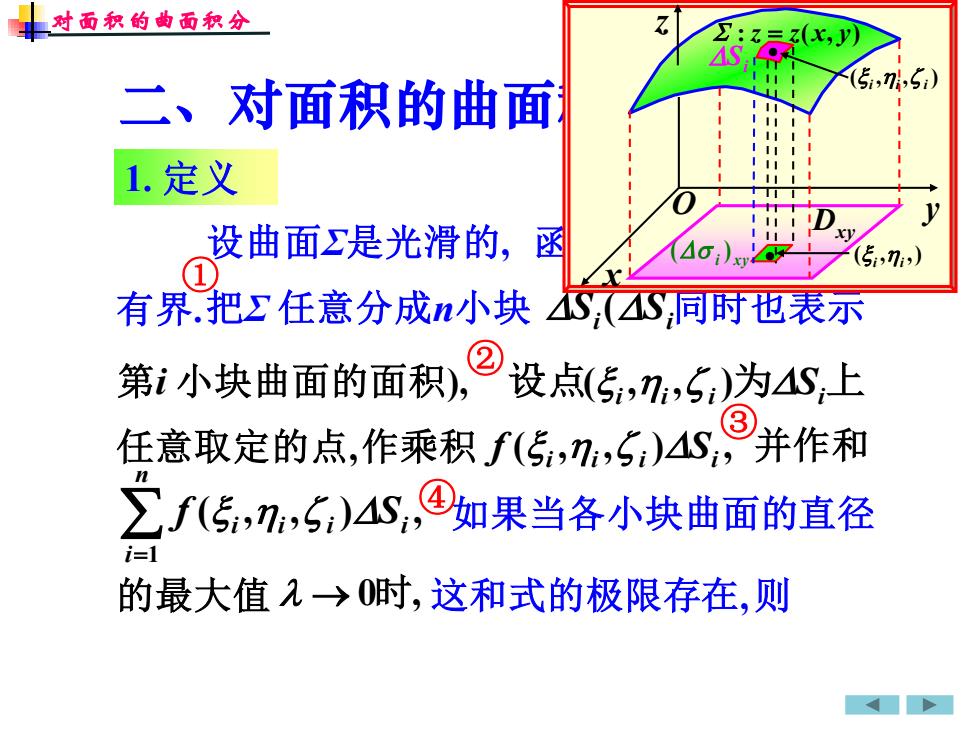
1. 定义 Si ( 设点( i ,i , i )为Si上 ( , , ) , i i i Si f ( , , ) , 1 i i i n i f i S = → 0时, Si 函数 f(x, y, z)在Σ上 任意取定的点, 并作和 如果当各小块曲面的直径 的最大值 这和式的极限存在,则 ① ② ③ ④ 对面积的曲面积分 二、对面积的曲面积分的定义 第i 小块曲面的面积), 作乘积 设曲面Σ是光滑的, 有界.把Σ 任意分成n小块 同时也表示 x O y z • • : z = z(x, y) ( , , ) i i i ( , ,) i i Si Dxy i xy ( )

对面积的曲面积分f(si,ni,Si)·4S,极限为函数 (x,J,z)在称i=1在曲面≥上对面积的曲面积分或JJ f(x,y,z)ds. 即第一类曲面积分.记为Z7Zf(5,ni,5.)AS;f(x, y,z)ds= lim2→0i=12积分曲面被积函数曲面元素9如曲面是闭曲面,则积分号写成
f (x, y,z)在 或 ( , , )d . 记为 f x y z S 即 如曲面是 被积函数 曲面元素 则积分号写成 i i i n i = f i S = → lim ( , , ) 1 0 f (x, y,z)dS 积分曲面 i i i n i f i S = ( , , ) 1 称 极限为函数 在曲面上 对面积的曲面积分 第一类曲面积分. 闭曲面, 对面积的曲面积分

对面积的曲面积分2.存在条件当f(x,,z)在光滑曲面上连续,对面积的曲面积分存在今后,假定f(x,J,z)在连续3.对面积的曲面积分的性质若可分为分片光滑的曲面及,则[[ f(x, y,z)dS =J] f(x, y,z)ds +[f f(x, y,z)dsZ21
若可分为分片光滑的曲面1及 2 ,则 2. 存在条件 在光滑曲面Σ上 今后,假定 1 ( , , )d f x y z S = f (x, y,z)dS 的曲面积分存在. 当f (x, y,z) 连续,对面积 f ( x, y,z)在上连续. 对面积的曲面积分 3. 对面积的曲面积分的性质 2 + d f x y z S ( , , )