
第一节二重积分的概念与性质问题的提出二重积分的概念二重积分的性质■小结思考题
第一节 二重积分的概念与性质 ◼ 问题的提出 ◼ 二重积分的概念 ◼ 二重积分的性质 ◼ 小结 思考题

问题的提出1·曲顶柱体的体积柱体体积=底面积×高平顶.特点:z= f(x,y柱体体积=?曲顶.特点:日曲顶柱体
柱体体积=底面积× 高 特点:平顶. 柱体体积=? 特点:曲顶. z = f (x, y) D 1.曲顶柱体的体积 一、问题的提出 曲顶柱体

“分割、求和、取求曲顶柱体的体积采用极限”的方法,如下动画演示。密放
播放 求曲顶柱体的体积采用 “分割、求和、取 极限”的方法,如下动画演示.
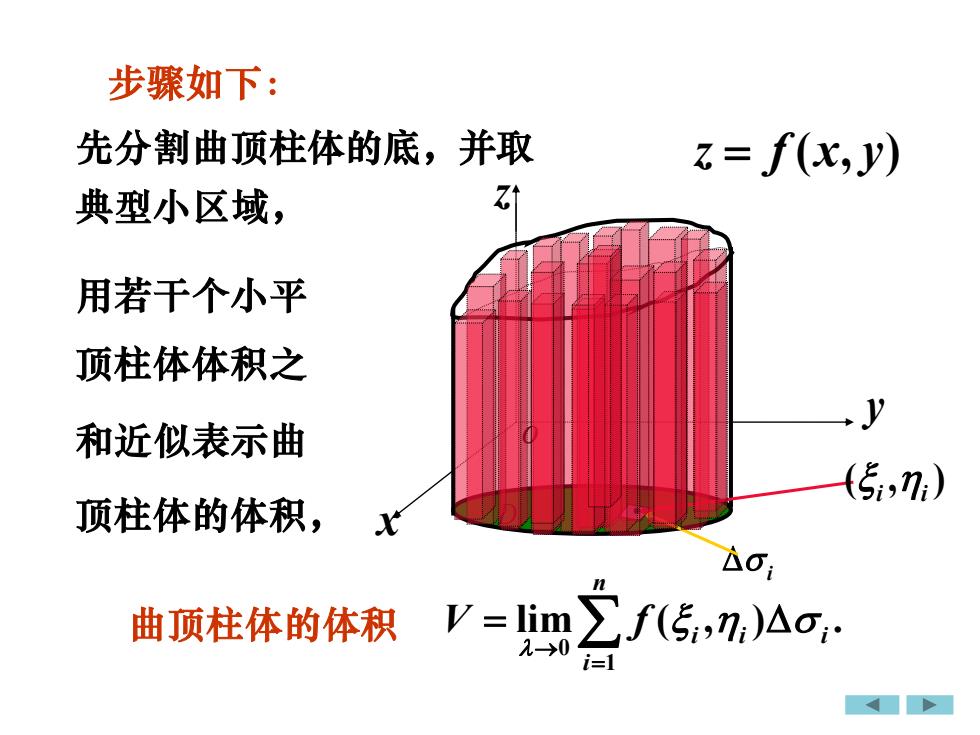
步骤如下:先分割曲顶柱体的底,并取z= f(x,y)Zt典型小区域用若干个小平顶柱体体积之y和近似表示曲(Si,n:)顶柱体的体积,△0;nZf(5,n,)A0.V = lim曲顶柱体的体积2-0i-1
步骤如下: 用若干个小平 顶柱体体积之 和近似表示曲 顶柱体的体积, x z y o D z f x y = ( , ) i • ( , ) i i 先分割曲顶柱体的底,并取 典型小区域, 0 1 lim ( , ) . n i i i i V f → = 曲顶柱体的体积 =
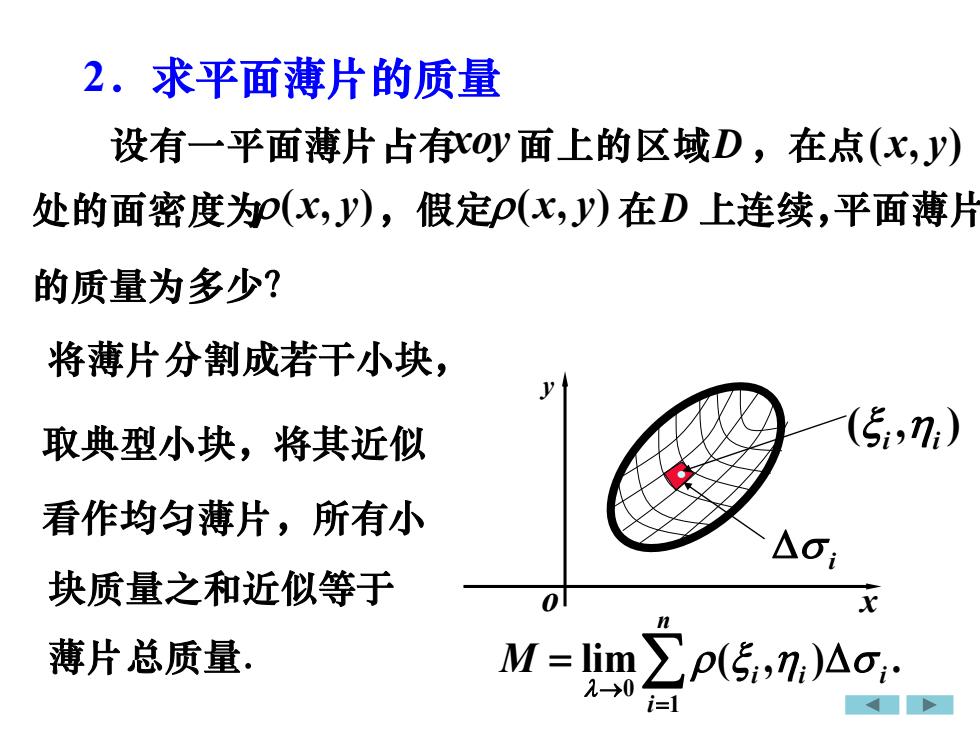
2.求平面薄片的质量设有一平面薄片占有xoy面上的区域D,在点(x,J)处的面密度为p(x,y),假定p(x,y)在D上连续,平面薄片的质量为多少?将薄片分割成若干小块(Si,n:)取典型小块,将其近似看作均匀薄片,所有小o;块质量之和近似等于olxZA薄片总质量M = limp(5i,n:)A,.2-→0i=1
2.求平面薄片的质量 i • ( , ) i i 将薄片分割成若干小块, 取典型小块,将其近似 看作均匀薄片,所有小 块质量之和近似等于 薄片总质量. 0 1 lim ( , ) . n i i i i M → = = x y o 设有一平面薄片占有 xoy 面上的区域 D ,在点 ( , ) x y 处的面密度为 ( , ) x y ,假定 ( , ) x y 在 D 上连续,平面薄片 的质量为多少?