
第一节多元函数的基本概念1预备知识多元函数的概念多元函数的极限多元函数的连续性小结思考题
第一节 多元函数的基本概念 ◼ 预备知识 ◼ 多元函数的概念 ◼ 多元函数的极限 ◼ 多元函数的连续性 ◼ 小结 思考题
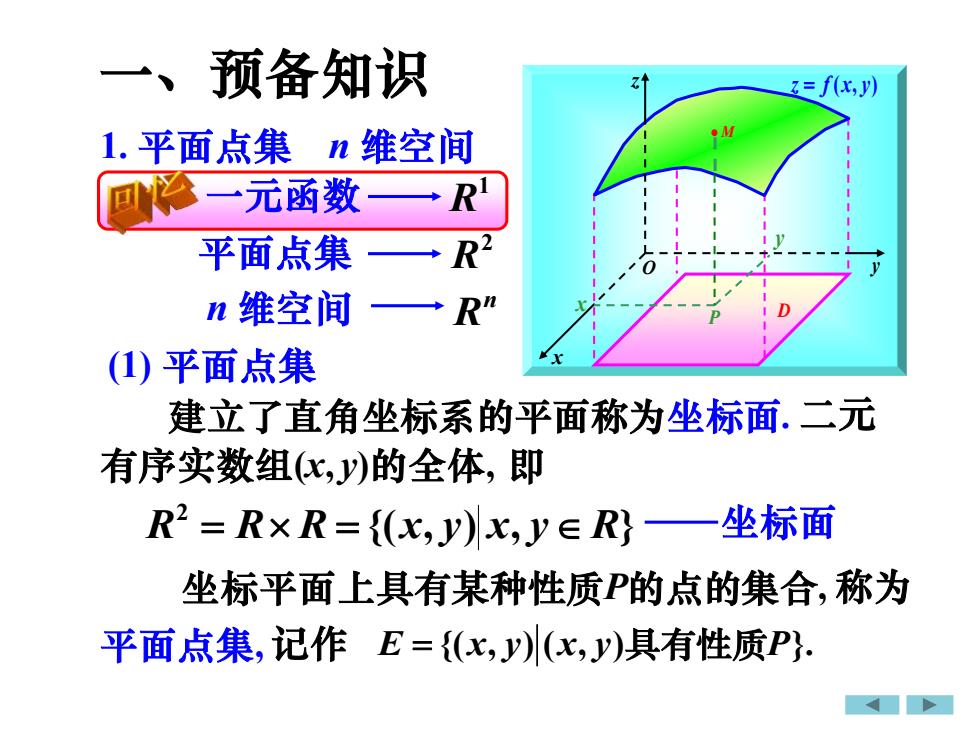
一、预备知识z= f(x,y)n维空间1.平面点集回之一元函数RR2平面点集n维空间R"|(1)平面点集建立了直角坐标系的平面称为坐标面.二元有序实数组(x,)的全体,即R2= R×R=(x,J)x,JE R)—坐标面坐标平面上具有某种性质P的点的集合,称为平面点集,记作E=(x,y)(x,J)具有性质P)
一、预备知识 1. 平面点集 n 维空间 一元函数 1 R 平面点集 2 R n 维空间 n R 有序实数组(x, y)的全体, 即 {( , ) , } 2 R = R R = x y x y R 建立了直角坐标系的平面称为坐标面. 坐标面 坐标平面上具有某种性质P的点的集合, 称为 平面点集, 记作 E x y x y P = {( , ) ( , ) }. 具有性质 (1) 平面点集 二元 D x y z O • M x y P z = f (x, y)
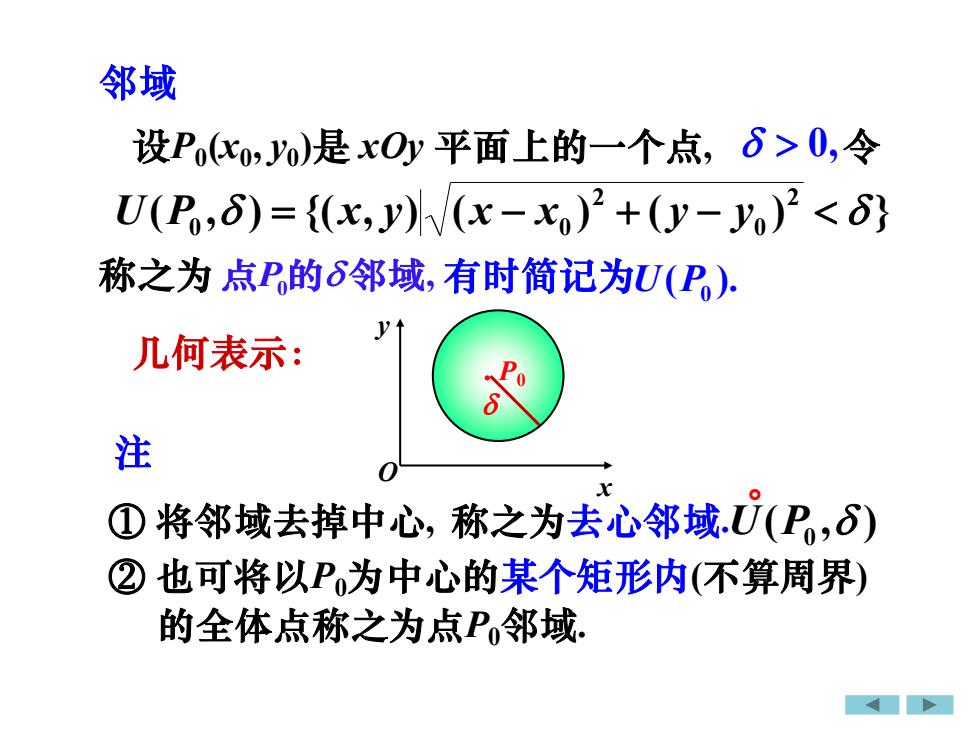
邻域设Po(xo,yo)是xOy平面上的一个点,>0,令U(P,8) =((x,y)/(x -x.)2 +(y- yo)2 <S)称之为点P的S邻域,有时简记为U(P)几何表示:注0①将邻域去掉中心,称之为去心邻域.U(P,S)②也可将以P为中心的某个矩形内(不算周界)的全体点称之为点P.邻域
邻域 设P0 (x0 , y0 )是 xOy 平面上的一个点, 几何表示: O x y . P0 ( , ) {( , ) ( ) ( ) } 2 0 2 U P0 = x y x − x0 + y − y 0 点P的邻域, 0, 令 ( ). 称之为 有时简记为 U P0 ① 将邻域去掉中心, ② 也可将以P0为中心的某个矩形内(不算周界) 注 称之为 的全体点称之为点P0邻域. 去心邻域. ( , ) U P0

任意一点PER2与任意一点集ER?之间必有以下三种关系中的一种:1)内点设E为一平面点集,点PeE,若存在S>0,使U(P)CE,称P为E的内点.(P)显然,E的内点属于E2)外点如果存在点P的某个邻域U(P)E使U(P)nE= Q,则称P为E的外点.(P)如点P的任一邻域内既有属于E的点3)边界点也有不属于E的点,称P为E的边界点.(P)E的边界点的全体称为E的边界,记作aE
1) 内点 显然, E的内点属于E. 点P E , 使U P E ( ) , E 2) 外点 如果存在点P的某个邻域 U(P), 则称P为E的外点. 3) 边界点 如点P的任一邻域内既有属于E的点, 也有不属于E的点,称P为E的边界点. 任意一点 2 P R 2 与任意一点集 E R 之间 必有以下三种关系中的一种: 设E为一平面点集, 0, 若存在 称P为E的内点. P1 • ( ) P1 ( ) P2 P2 • P3 • ( ) P3 E的边界点的全体称为E的边界, 记作 E. 使U(P) ∩ E =

聚点如果对于任意给定的S>0.点P的去心邻域U(P,)内总有E中的点(P本身可属于E,也可不属于E),则称P是E的聚点例如,设点集 E=((x,y)1≤x2+2<2)点P(xo,o) R2,若1<x+%<2,则P为E的内点;若x+=1 或x+=2,则P为E的边界点,也是E的聚点E的边界aE为集合(x, y)x? + y2 = 1)U((x,y)x? + y? = 2)
聚点 如果对于任意给定的 0, 点P的去心邻域 U(P, ) 内总有E中的点 则称P是E的聚点. 例如, 设点集 (P本身可属于E,也可不 属于E ), {( , )1 2}, 2 2 E = x y x + y ( , ) , 2 点P x0 y0 R 2 2 0 0 若1 2, + x y 则P为E的内点; 2 2 0 0 若 x y + = 1 2 2 0 0 或 x y + = 2, 则P为E的边界点, 也是E的聚点. E的边界 E 为集合 {( , ) 1} {( , ) 2}. 2 2 2 2 x y x + y = x y x + y =