
第一节对弧长的曲线积分对弧长的曲线积分的概念与性质11 111 对弧长的曲线积分的计算法几何与物理意义四、小结思考题
第一节 对弧长的曲线积分 一、对弧长的曲线积分的概念与性质 二、对弧长的曲线积分的计算法 三、几何与物理意义 四、小结 思考题
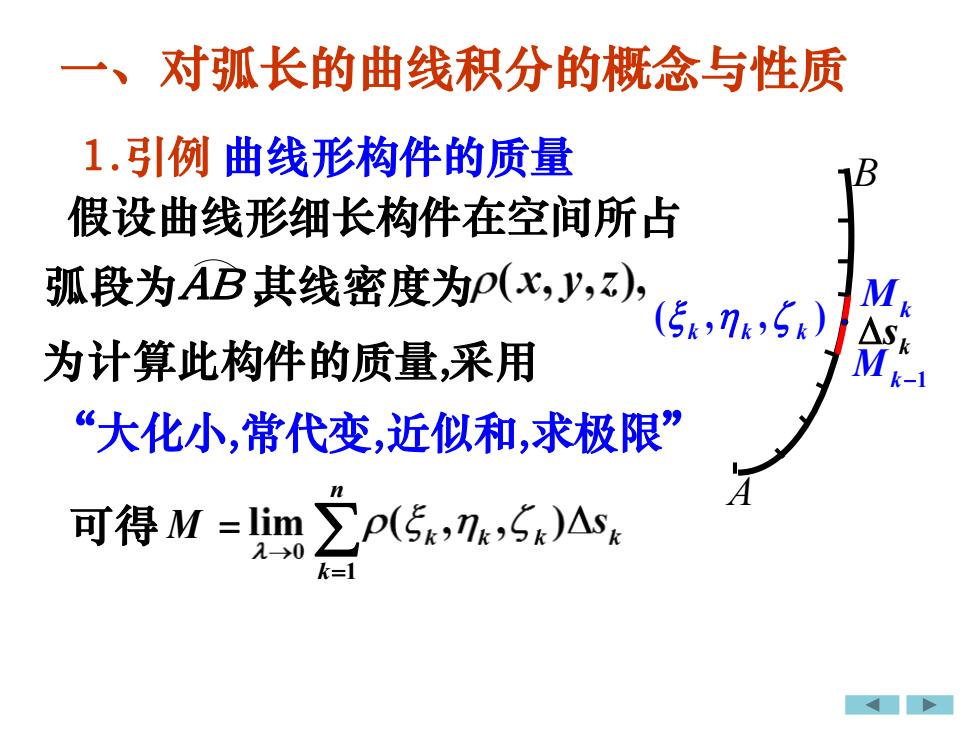
对弧长的曲线积分的概念与性质一、1.引例曲线形构件的质量1B假设曲线形细长构件在空间所占弧段为AB其线密度为p(x,y,z),M(Ek,nk,Sh)AsM为计算此构件的质量,采用k-1“大化小,常代变,近似和,求极限”A1Zp(5k,n,S)Ask可得M =lim2>0k=1
A B 一、对弧长的曲线积分的概念与性质 假设曲线形细长构件在空间所占 弧段为AB , 其线密度为 “大化小,常代变,近似和,求极限” 可得 1 n k= M = 为计算此构件的质量, k s Mk −1 Mk ( , , ) k k k 1.引例 曲线形构件的质量 采用

2.定义设I是空间中一条有限长的光滑曲线,f(x,y,z)是定义在I上的一个有界函数(5k,nk,Sk)若通过对I的任意分割和对局部的任意取点下列“乘积和式极限M记作nlimEf(5k,nk,5h)AsAs f(x,y,z)dsM1-→0k-1k=1r
设是空间中一条有限长的光滑曲线, 义在上的一个有界函数, ( , , ) k k k k f s = 记作 f x y z s ( , , ) d 若通过对的任意分割 局部的任意取点, 2. 定义 下列“乘积和式极限” 1 n k= lim →0 k s Mk −1 Mk ( , , ) k k k 和对

都存在,则称此极限为函数f(x,,z)在曲线厂上对弧长的曲线积分或第一类曲线积分f(x,y,z)称为被积函数,I称为积分弧段曲线形构件的质量M =_p(x,y,z)ds
都存在, 上对弧长的曲线积分, 则称此极限为函数 在曲线 或第一类曲线积分. 称为被积函数,称为积分弧段. 曲线形构件的质量 M x y z s ( , , ) d =

如果L是xoy面上的曲线弧,则定义对弧长的曲线积分为Zf(5n,n)Ask[,f(x,y)ds =lim1→0k=1如果 L是闭曲线,则记为Φ,f(x,y)ds.思考(1)若在L上f(x,y)=l,(,ds 表示什么 ?(2)定积分是否可看作对弧长曲线积分的特例?否!对弧长的曲线积分要求ds≥0,但定积分中dx可能为负
如果L是xoy面上的曲线弧, 0 1 lim ( , ) n k k k k f s → = L f x y s ( , )d = 如果 L是闭曲线, 则记为 ( , ) d . L f x y s 则定义对弧长的 曲线积分为 思考 (1) 若在L上 f(x,y)≡1, d ? L s 表示什么 (2) 定积分是否可看作对弧长曲线积分的特例? 否! 对弧长的曲线积分要求ds 0,但定积分中 dx可能为负