
第五章 定积分 高等数学少学时 第五章定积分 第一节 定积分的概念与性质 第二节 微积分基本公式 第三节 定积分的计算方法 第四节 广义积分 第五节 定积分在几何中的应用 第六节 定积分在物理学中的应用 第五章 习题课 北京邮电大学出版社
1 第五章 定积分 第一节 定积分的概念与性质 第二节 微积分基本公式 第三节 定积分的计算方法 第四节 广义积分 第五节 定积分在几何中的应用 第六节 定积分在物理学中的应用 第五章 习题课

第五章定积分 高等数学少学时 第一节定积分的桃念与性质 一、定积分的概念 二、定积分的性质 北京邮电大学出版社
2 第一节 定积分的概念与性质 一、定积分的概念 二、定积分的性质

第五章 定积分 高等数学少学时 一、定积分的概念 y=f(x) 1.引例1曲边梯形的面积 (1)曲边梯形的定义 设Jy=fx)在闭区间[a,b]上非负,连续.Ox=a x=bx 由直线x=4,x=by=0及曲线y=fx)所围 成的图形称为曲边梯形,其中曲线弧称为曲边 矩形面积=ah 曲边梯形面积S=? 梯形面积=(a+b) 北京邮电大学出版社 3
3 一、定积分的概念 1.引例1 曲边梯形的面积 (1)曲边梯形的定义 y = f (x) x = a x = b x y O 由直线 x= a, x= b, y= 0及曲线 y= f (x)所围 成的图形称为曲边梯形,其中曲线弧称为曲边. 设 y= f(x) 在闭区间 [a,b] 上非负, 连续. 矩形面积 梯形面积 曲边梯形面积S=?
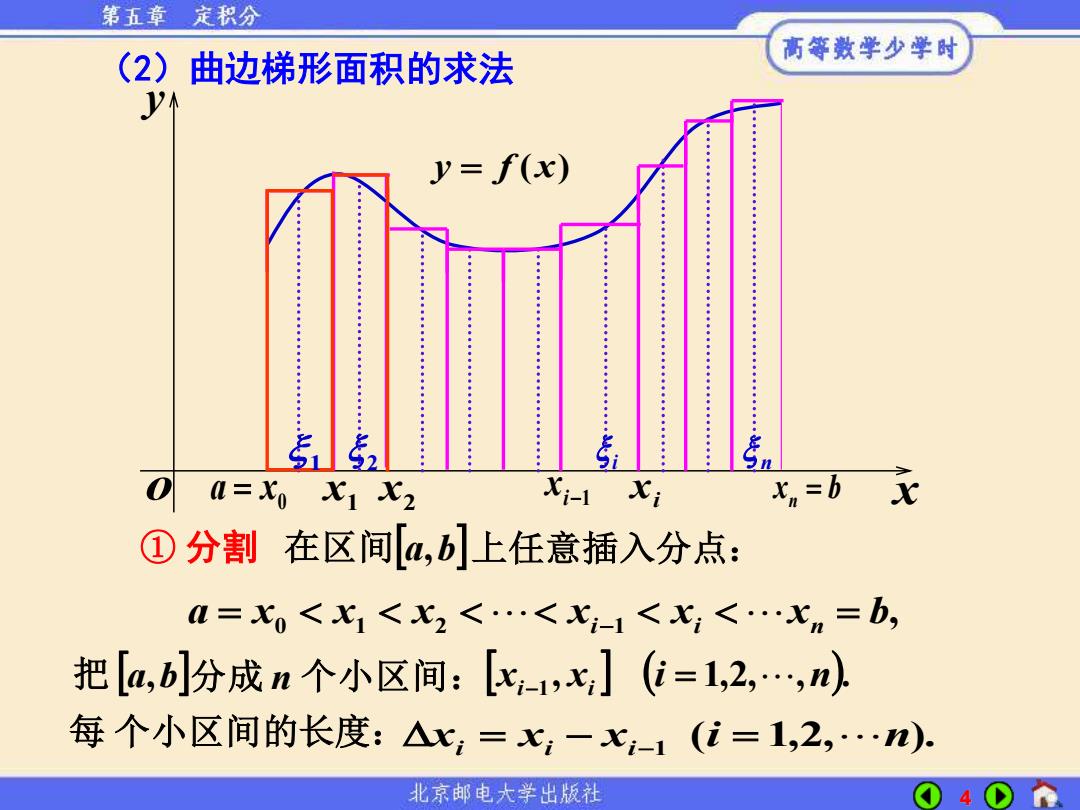
第五章定积分 (2)曲边梯形面积的求法 高等数学少学时 y=f(x) 0 0=x0x1X2 Xi-1 Xi x=b ①分割在区间4,b]上任意插入分点: M=X0<X1<X2<…<X;-1<X,<…Xn=b, 把[a,b]分成n个小区间:[x-1,x](i=1,2,,) 每个小区间的长度:△x:=x;-x-1(i=1,2,…n) 北京邮电大学出版社 4
4 , a = x0 x1 x2 xi−1 xi xn = b ① 分割 ( 1,2, ). xi = xi − xi−1 i = n 在区间 a,b 上任意插入分点: 每 个小区间的长度: (2)曲边梯形面积的求法 x y y = f (x) o 0 a = x x1 xi x b n = x2 i−1 x , ( 1,2, , ). 把 a,b 分成 n 个小区间: xi−1 xi i = n 1 2 i n
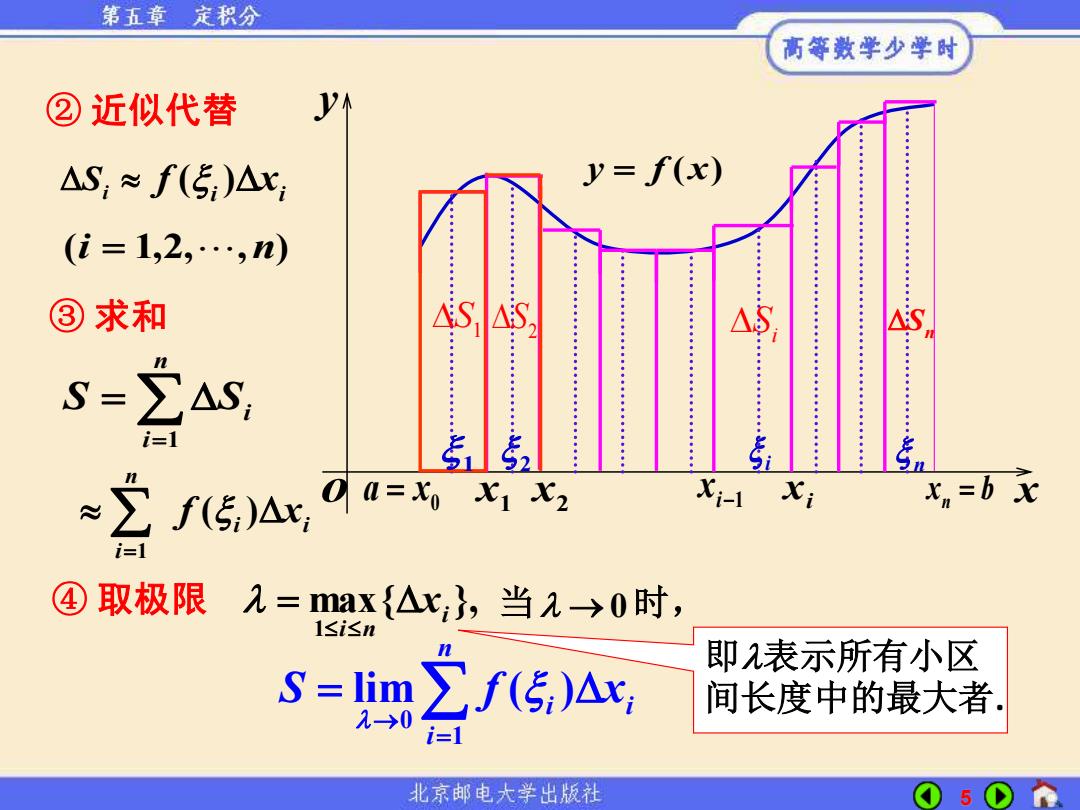
第五章 定积分 高等数学少学时 ②近似代替 △S,≈f(5:)△x: y=f(x) (i=1,2,…,n) ③求和 S△S, S-∑AS, i=1 51 52 ≈∑f传)A,0a=x Xi-1 Xi x,=bx i=1 ④取极限 2=max{△x;},当2-→0时, 1si<n 即λ表示所有小区 S=lim ∑f(5)△, 间长度中的最大者 -→0 i= 北京邮电大学出版社 5
5 x y y = f (x) o 0 a = x x1 xi x b n = x2 i−1 x 1 2 i n 1 S 2 S i S Sn 1 n i i S S = = Si ② 近似代替 ( )i i f x 1 ( ) n i i i f x = ③ 求和 (i = 1,2, ,n) ④ 取极限 max{ }, 1 i i n = x 0 1 lim ( ) n i i i S f x → = = 即表示所有小区 间长度中的最大者. 当 → 0 时