
第五章 定积分 高等数学少学时 直角坐标 s=∫[f(x)-g(x]de s=[p(y)-w(y)]4 复习 一、 面积 参数方程S=∫yde=∫y()p'(t)dt 极坐标系 s=[p(o)]d6 平行截面面积已知的立体V=S(x)dr 二、体积 旋转体 .=∫[fx]'d ',=∫[p(]'d 直角坐标s=∫1+d 三、弧长 参数方程 s=∫Vp2()+y2(t)d 北京邮电大学出版社
1 b x a V f x x 2 = ( ) d b a V S x x = ( )d 二、体积 平行截面面积已知的立体 旋转体 2 π ( ) d d y c V y y = 2 1 ' d b a s y x = + 2 2 s t t t = + ' ( ) ' ( )d 三、弧长 直角坐标 参数方程 b a S f x g x x = − ( ) ( ) d ( ) 1 2 d 2 S = 一、面积 极坐标系 直角坐标 参数方程 b a S y x t t t = = d ( ) ( )d ( ) ( ) d c S y y y = − d 复习

第五章定积分 高等数学少学时 第六节定积分在物理学中的定用 一、变力沿直线所做的功 二、水压力 三、其他应用 北京邮电大学出版社
2 第六节 定积分在物理学中的应用 一、变力沿直线所做的功 三、其他应用 二、水压力

第五章 定积分 高等数学少学时 一、变力沿直线所做的功 F(x) 恒力作功:W=F·S xx+dx b x 设有一变力Fx)随位移x而变, 求它把物体由a移动到b所作的功. 取x为积分变量,它的变化区间为,b]在此区间上任取 小区间[,x+dx,在此小区间上变力所作的功近似等于以x点的 力为恒力所作的功,这个小区间功的近似值即为功元素,即 功元素为: dW=F(x)dx 于是所作的功为 W=∫F(x)d 北京邮电大学出版社 3
3 W = F s 取 x为积分变量,它的变化区间为[a, b],在此区间上任取 小区间[x, x+dx], 力为恒力所作的功, 在此小区间上变力所作的功近似等于以x点的 d ( )d W F x x = ( )d b a W F x x = • • x x+dx • • • O a b x F(x) 一、变力沿直线所做的功 恒力作功: 这个小区间功的近似值即为功元素,即 功元素为: 于是所作的功为 求它把物体由a 移动到 b 所作的功. 设有一变力F(x)随位移x而变
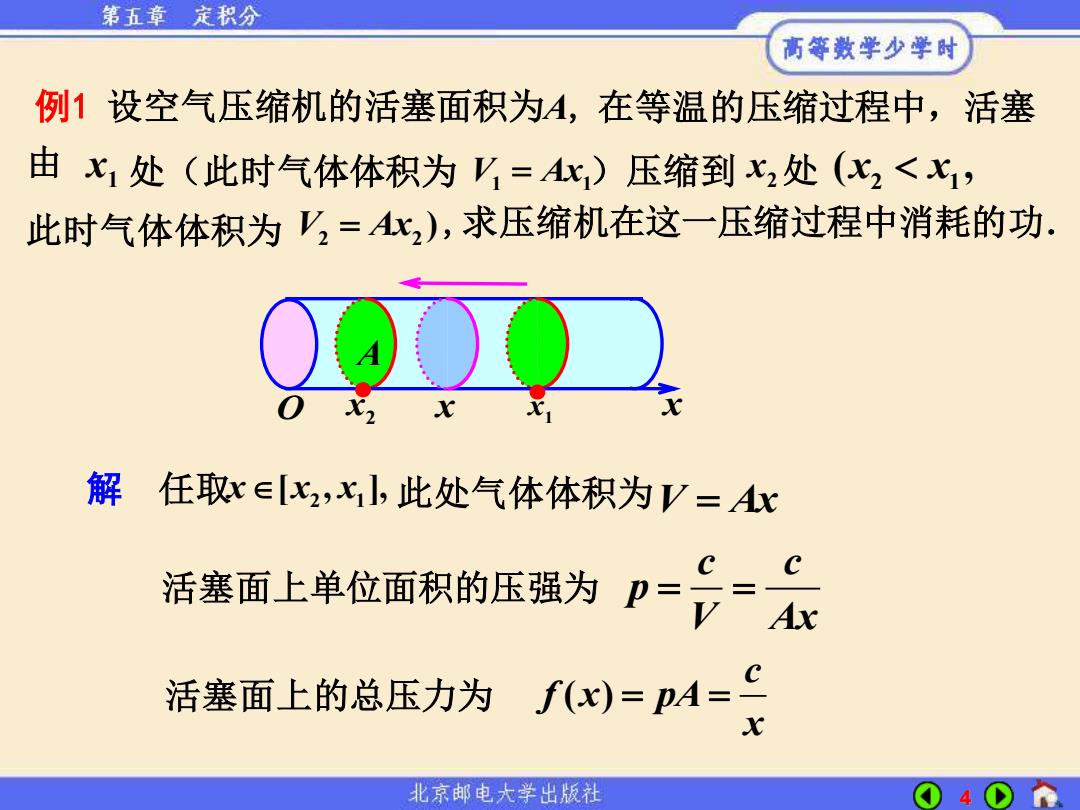
第五章 定积分 高等数学少学时 例1设空气压缩机的活塞面积为A,在等温的压缩过程中,活塞 由x1处(此时气体体积为V=Ax)压缩到x2处(x2<x1, 此时气体体积为V,=A比,),求压缩机在这一压缩过程中消耗的功. 解 任取x∈[x2,x,此处气体体积为V=Ax C 活塞面上单位面积的压强为 p= Ax 活塞面上的总压力为 f(x)=pA=c x 北京邮电大学出版社
4 V Ax = c c p V Ax = = c f x pA x ( ) = = 2 1 解 任取 x x x [ , ], 此处气体体积为 活塞面上单位面积的压强为 活塞面上的总压力为 此时气体体积为 x1 V Ax 1 1 = x2 V Ax 2 2 = ) 例1 设空气压缩机的活塞面积为A, 在等温的压缩过程中,活塞 处(此时气体体积为 )压缩到 处 ,求压缩机在这一压缩过程中消耗的功. x x 2 1 ( , x2 x O 1 x • • A x 由

第五章 定积分 高等数学少学时 于是在点x处压缩机消耗的功元素为 dw-Cdx c 压缩过程中所消耗的功为 w-aw-fsa-em x X2 北京邮电大学出版社 05C
5 d d c W x x = 1 1 2 2 1 2 d d ln x x x x c x W W x c x x = = = 于是在点x处压缩机消耗的功元素为 压缩过程中所消耗的功为