
第三章 微分中值定理与导数的应用 高等数学少学时 第五节品数的极值 与最大值最小值 一、函数的极值及其求法 二、函数的最大最小值问题 北京邮电大学出版社
1 第五节 函数的极值 与最大值最小值 一、函数的极值及其求法 二、函数的最大最小值问题

第三章微分中值定理与导数的应用 高等数学少学时 一、函数的极值及其求法 定义设函数f(x)在区间(,b)内有定义,x。∈(a,b). 如果存在着点x,的一个去心邻域,从这去心邻域内任取一点 x,都有f(x)<f(x)(f(x)>f(x),那么称f(x)是函数 f(x)的一个极大小值. 函数的极大值与极小值统称为函数的极值,使函数取得 极值的点称为极值点. 函数的极大值和极小值的概念是局部性的.如下图 北京邮电大学出版社 2
2 一、函数的极值及其求法 定义 设函数 f x( ) 在区间 ( , ) a b 内有定义, 0 x a b ( , ). 如果存在着点 0 x 的一个去心邻域, 从这去心邻域内任取一点 x, 函数的极大值与极小值统称为函数的极值,使函数取得 极值的点称为极值点. 函数的极大值和极小值的概念是局部性的.如下图 都有 0 f x f x ( ) ( ) 0 ( ( ) ( )), f x f x 那么称 0 f x( ) 是函数 f x( ) 的一个极大(小)值
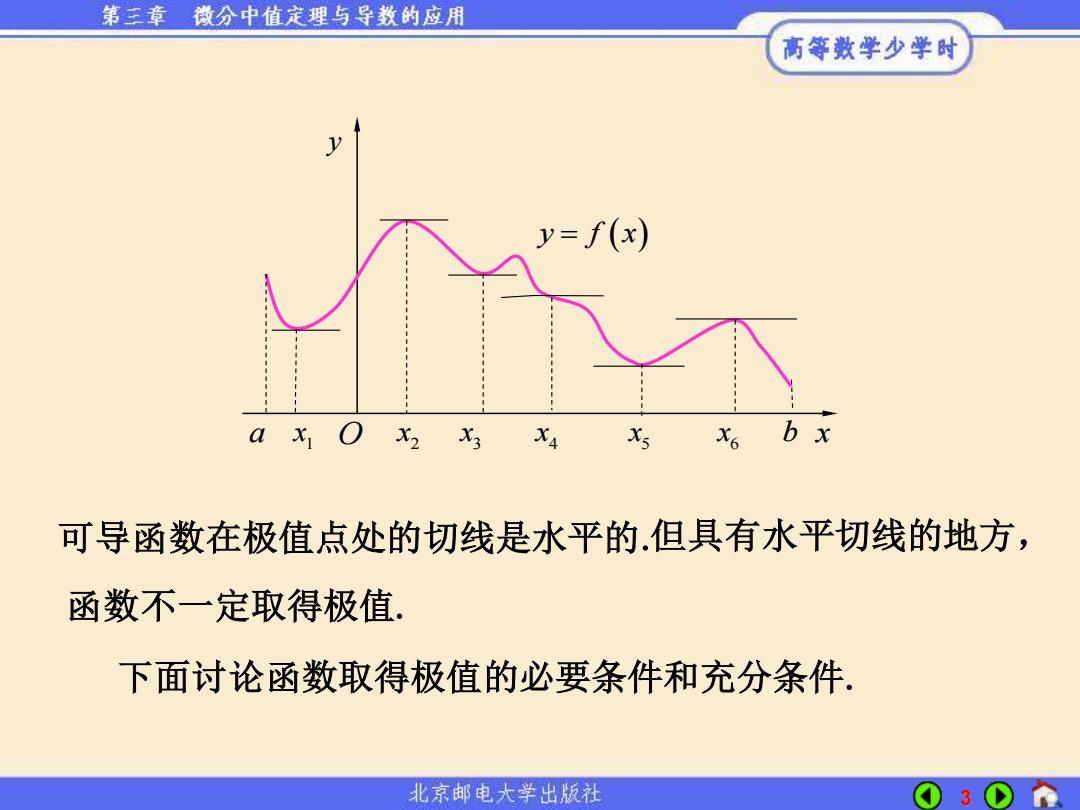
第三章 微分中值定理与导数的应用 高等数学少学时 y=f(x) x6 b x 可导函数在极值点处的切线是水平的.但具有水平切线的地方, 函数不一定取得极值. 下面讨论函数取得极值的必要条件和充分条件. 北京邮电大学出版社 3
3 可导函数在极值点处的切线是水平的. 函数不一定取得极值. 但具有水平切线的地方, 下面讨论函数取得极值的必要条件和充分条件. a x1 O x2 x3 x4 x5 x6 b y f x = ( ) y x

第三章 微分中值定理与导数的应用 高等数学少学时 定理1(必要条件)设函数f(x)在点x,处可导,且在x 处取得极值,那么f'(x)=0. 证设f(x)是极大值.由于函数f(x)在点x。处可导, 根据导数定义"(x,)=im f(x)-f() x-x0 x-xo x<时,f-),o因此mf)-(之 x-xo x→x0 x-xo x>时, (x-fx】<0 因此lim f(s)-f(x≤0. x-xo x→x0 x-xo 故f'()=0. 使得导数等于零的点(即方程'(x)=0的实根),叫做函数 f(x)的驻点. 北京邮电大学出版社
4 定理1(必要条件) 设函数 f (x) 在点 0 x 处可导,且在 0 x 处取得极值,那么 f x ( 0 ) = 0. 证 设 f x( 0 ) 是极大值. 由于函数 f (x) 在点 0 x 处可导, 根据导数定义 ( ) ( ) ( ) 0 0 0 0 lim . x x f x f x f x → x x − = − 0 x x 时, ( ) ( 0 ) 0 0 f x f x x x − − 因此 ( ) ( ) 0 0 0 lim 0; x x f x f x x x → − − − 0 x x 时, ( ) ( 0 ) 0 0 f x f x x x − − 因此 ( ) ( ) 0 0 0 lim 0. x x f x f x x x → − − − 故 f x ( 0 ) = 0. 使得导数等于零的点(即方程 f x ( ) = 0 的实根),叫做函数 f x( ) 的驻点
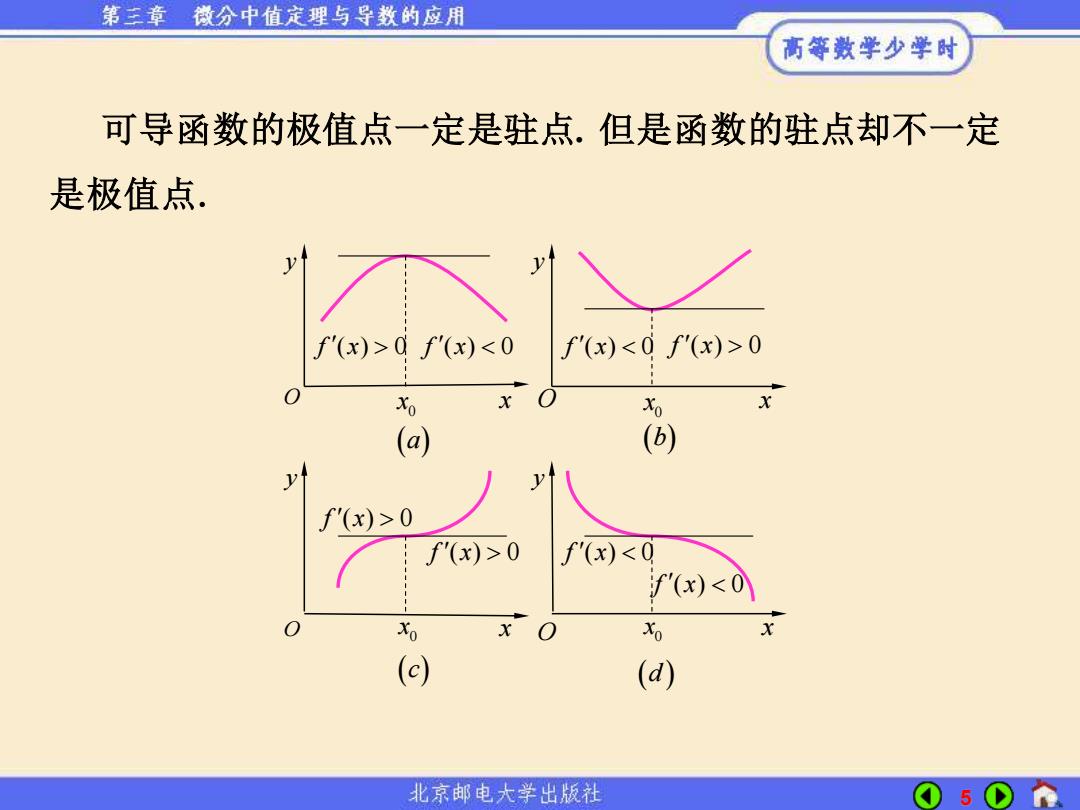
第三章 微分中值定理与导数的应用 高等数学少学时 可导函数的极值点一定是驻点.但是函数的驻点却不一定 是极值点. y f'(x)>0f'(x)<0 f'(x)<0f'(x)>0 Xo X 0 (a) (b) f)>0 f'(x)>0 f'(x)<0 f'(x)<0 Xo O 0 (c) (d) 北京邮电大学出版社 5
5 可导函数的极值点一定是驻点. 但是函数的驻点却不一定 是极值点. O O O O x x x y y y y 0 x 0 x 0 x 0 x x (a) (b) (c) (d ) f x ( ) 0 f x ( ) 0 f x ( ) 0 f x ( ) 0 f x ( ) 0 f x ( ) 0 f x ( ) 0 f x ( ) 0