
第三章 微分中值定理与导数的应用 高等数学少学时 第三章微分中值交理 与导数的爱用 第一节 微分中值定理 第二节 洛必达法则 第三节 泰勒公式 第四节 函数的单调性与曲线的凹凸性 第五节 函数的极值与最大值最小值 第六节 方程的近似解 北京邮电大学出版社
1 第一节 微分中值定理 第三章 微分中值定理 第二节 洛必达法则 第三节 泰勒公式 第四节 函数的单调性与曲线的凹凸性 第五节 函数的极值与最大值最小值 第六节 方程的近似解 与导数的应用

第三章 微分中值定理与导数的应用 高等数学少学时 第一节微分中值定理 一、罗尔(RolIe)定理 二、拉格朗日(Lagrange)中值定理 三、柯西(Cauchy)中值定理 北京邮电大学出版社
2 一、罗尔(Rolle)定理 二、拉格朗日(Lagrange)中值定理 三、柯西(Cauchy)中值定理 第一节 微分中值定理

第三章微分中值定理与导数的应用 高等数学少学时 一、罗尔(Rolle)定理 fx)满足: B (1)在区间[a,b]上连续; A (2)在区间(a,b)内可导; a (3)f(M)=f(b), >在(a,b)内至少存在一点5,使f'(5)=0. 证因为f(x)在[a,b]上连续,故在[a,b]上取得最大值M 和最小值m. 若M=m,则f(x)≡M,x∈[a,b], 因此5∈(a,b),f'()=0. 北京邮电大学出版社 03
3 一、罗尔(Rolle)定理 f (x)满足: (1) 在区间 [a , b] 上连续; (2) 在区间 (a , b) 内可导; (3) f ( a ) = f ( b ), 证 故在 [a , b] 上取得最大值 M 和最小值 m . 若 M = m , 则 因此 在( a , b ) 内至少存在一点 因为 f (x) 在 [a, b] 上连续, y O a b A B C x f x M x a b ( ) , [ , ] , ,使f ( ) = 0

第三章 微分中值定理与导数的应用 高等数学少学时 若M>m,则M和m中至少有一个与端点值不等, 不妨设M≠f(a),则至少存在一点5∈(a,b),使 f(5)=M,下面证明f'(E)=0. y 因为f(x)在5∈(a,b)处可导,所以 B A f(5)=lim f(5+△x)-f(5) △x0 △x a =∫f≥0(4x→0) =f5)≤0(ax→0) >f'(5)=0. 北京邮电大学出版社
4 若 M > m , 则 不妨设 则至少存在一点 使 下面证明 因为 f x( ) 在 处可导, 所以 M 和 m 中至少有一个与端点值不等, y O a b A B C x M f a ( ) , ( , ), a b f M ( ) , = f ( ) 0. = ( 0 ) x − → 0 ( 0 ) x + → f ( ) 0. =
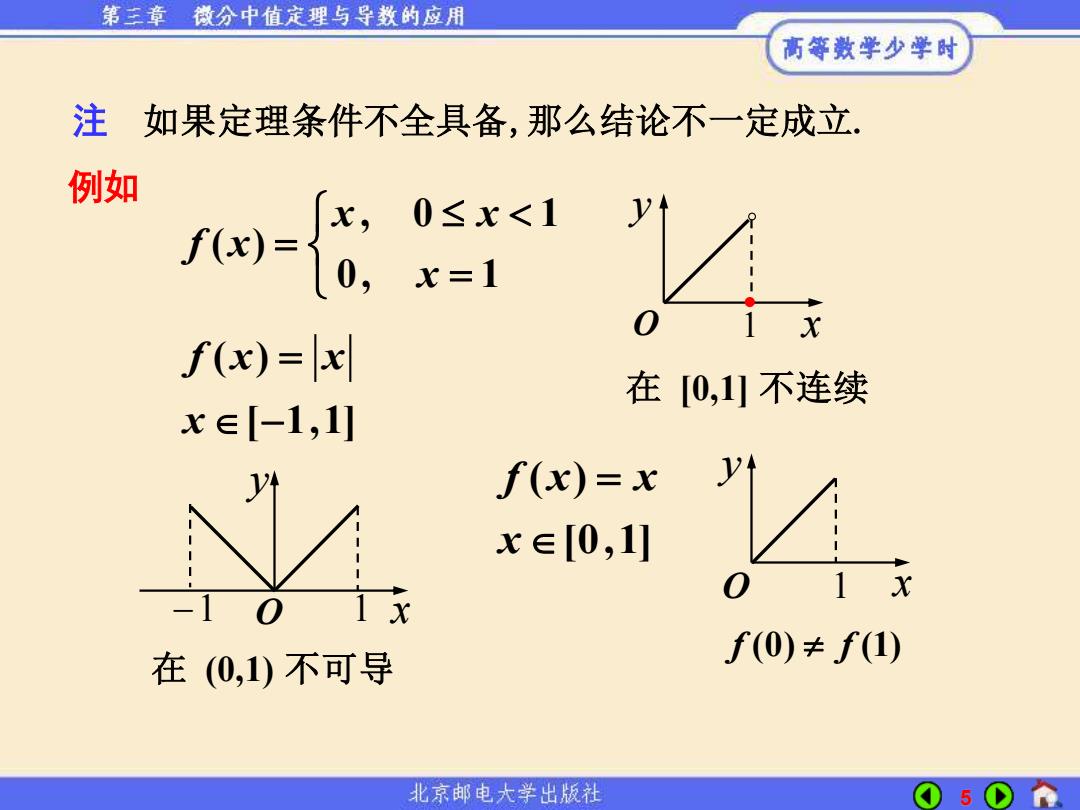
第三章微分中值定理与导数的应用 高等数学少学时 注如果定理条件不全具备,那么结论不一定成立 例如 x,0≤x<1 f)={0,x=1 f(x)=x 在[0,1山不连续 x∈[-1,1] f(x)=x y x∈[0,1] 0 X 1 x 在(0,1)不可导 北京邮电大学出版社 5
5 注 如果定理条件不全具备,那么结论不一定成立. 例如 在 [0,1] 不连续 1 x y −1 O 1 x y O f f (0) (1) 1 x y O 在 (0,1) 不可导 , 0 1 ( ) 0, 1 x x f x x = = ( ) [ 1,1] f x x x = − ( ) [0,1] f x x x =