
第五章定积分 高等数学少学时 第四节广义积分 一、无穷限的广义积分 二、无界函数的广义积分 北京邮电大学出版社 10
1 二、无界函数的广义积分 一、无穷限的广义积分 第四节 广义积分

第五章 定积分 高等数学少学时 一、无穷限的广义积分 定义1设f(x)eC[a,+o), 对于vb>a,如果 I=limIf(x)dx 则称此极限为(x)在[a,+o)上的广义积分,记作∫fx)dx, 即 fxdk=m心fxdr (1) 此时也称广义积分。f(x)dx收敛; 如果上述极限不存在, ∫f(x)dc就没有意义,习惯上称广义积分f(x)dc发散, 这时f(x)dr也就不再表示数值了. 北京邮电大学出版社 2
2 一、无穷限的广义积分 定义1 如果 lim d ( ) b b a I f x x →+ = 则称此极限为 f x a ( ) , 在 +) 上的广义积分, 记作 ( )d , a f x x + 即 设 f (x)Ca,+), 对于b a, 此时也称广义积分 ( )d a f x x + 收敛; 如果上述极限不存在, ( )d a f x x + 就没有意义,习惯上称广义积分 ( )d a f x x + 发散, ( )d a f x x + 这时 也就不再表示数值了. ( )d lim ( )d b a a b f x x f x x + →+ = (1) a x y O b

第五章定积分 高等数学少学时 类似地 设f(x)∈C(-∞,b,Va<b,如果 I lim ['f(x)dx 100 则称此极限为.f(x)在(-o,b上的广义积分,记作∫fx)c, 即 ∫fx)d=Iim∫fx)dc (2) 这时也称广义积分f(x)dr收敛;否则称f(x)dr发散. 注为书写方便记∫f(x)r=[F()].=F(b)-IimF(x) 00 北京邮电大学出版社 3
3 如果 1 lim ( )d b a a I f x x →− = 则称此极限为 f x( ) 在 ( , ] − b 上的广义积分, 记作 ( )d , b f x x − 即 这时也称广义积分 ( )d b f x x − 收敛; 否则称 ( )d b f x x − 发散. 类似地 设 f (x)C(− ,b], a b, 注 ( )d ( ) ( ) lim ( ) b b x f x x F x F b F x − − →− = = − 为书写方便记 ( )d lim ( )d b b a a f x x f x x − →− = (2)
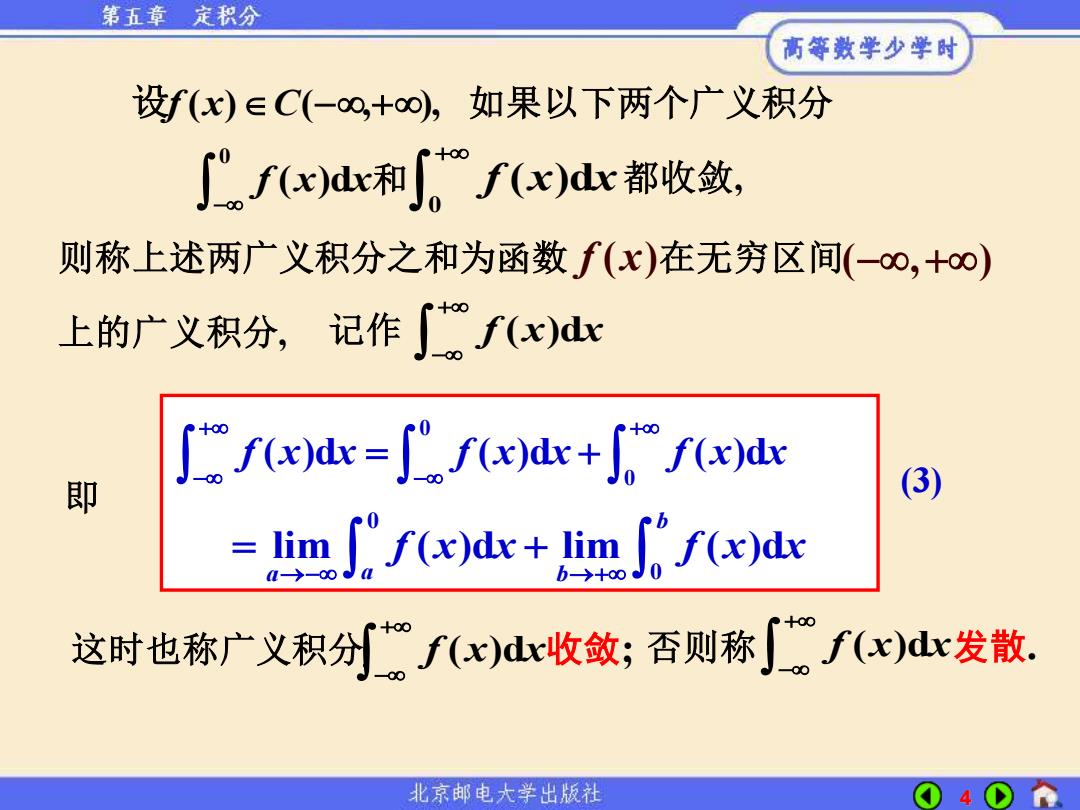
第五章 定积分 高等数学少学时 设f(x)∈C(-o∞,+o),如果以下两个广义积分 ∫nf(x)de和f(e)dc都收敛, 则称上述两广义积分之和为函数f(x)在无穷区间(-0,+o) 上的广义积分,记作」fx)dc ∫fx)ac=Jnfe)dc+fxdr 即 (3) =imJf(x)dc+m∫fe)dc 这时也称广义积分f(x)d收敛;否则称」f(x)dr发散. 北京邮电大学出版社
4 如果以下两个广义积分 0 f x x ( )d − 和 0 f x x ( )d + 都收敛, 即 这时也称广义积分 f x x ( )d + − 收敛; 否则称 f x x ( )d + − 发散. ( , ) − + 上的广义积分, 则称上述两广义积分之和为函数 f x( ) 在无穷区间 f x x ( )d + − 记作 设f (x)C(−,+),0 0 f x x f x x f x x ( )d ( )d ( )d + + − − = + 0 0 lim ( )d lim ( )d b a b a f x x f x x →− →+ = + (3)

第五章 定积分 高等数学少学时 1 例1计算由曲线y= 2 直线x=1及x轴所围成的开口 曲边梯形的面积. 解由定积分的几何意义,开口曲边梯形的面积 -照[- 北京邮电大学出版社 05
5 2 1 dx A x + = 2 1 d lim b b x → + x = 1 1 lim b b→ + x = − 1 lim 1 b→ + b = − 解 由定积分的几何意义,开口曲边梯形的面积 2 1 y x 例1 计算由曲线 = ,直线 x = 1 及 x 轴所围成的开口 曲边梯形的面积. = 1