复变函数如果我们把这两条简单闭曲线C及C-看成一条复合闭路I,「的正方向为外面的闭曲线C按逆时针进行内部的闭曲线C,按顺时针进行(即沿I的正向进行时,I的R内部总在I的左手边)那说明:在变形过程中曲线不经A过函数z)的不解析的点解析函数,曲线的积分,不因闭曲线在区域内作连续变形而改变它的值.闭路变形原理u
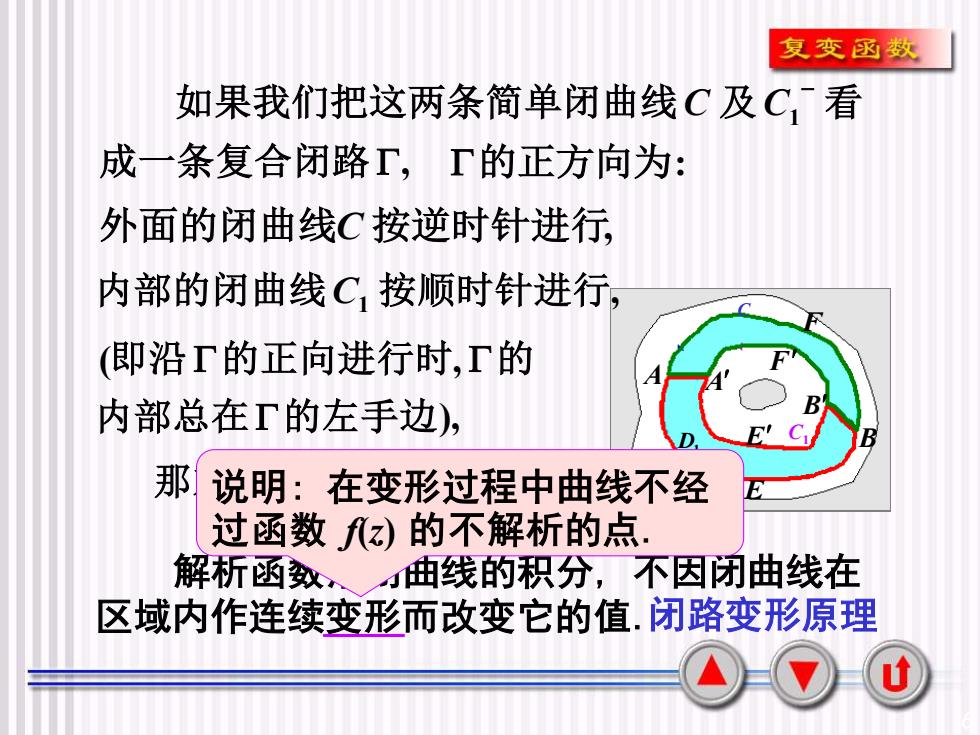
6 D C C1 D1 A A B B E E F F , 1 − 成一条复合闭路 如果我们把这两条简单闭曲线C 及C 看 的正方向为: 外面的闭曲线C 按逆时针进行, , 内部的闭曲线C1 按顺时针进行 ), ( , 内部总在 的左手边 即沿 的正向进行时 的 ( ) = 0. 那末 f z dz 解析函数沿闭曲线的积分, 不因闭曲线在 区域内作连续变形而改变它的值.闭路变形原理 说明: 在变形过程中曲线不经 过函数 f(z) 的不解析的点

复变函数2.复合闭路定理设C为多连通域D内的一条简单闭曲线C,C2,C,是在C内部的简单闭曲线它们互不包含也互不相交并且以C,C1,C2··",C,为边界的区域全含于D如果,f(z)在D内解析C3C那末DZf(1)f (z)dz =)f(z)dz,JCk=1L其中C及C.均取正方向u
7 2. 复合闭路定理 , , , , , , , , , , , 1 2 1 2 D C C C C C C C C C D n n 为边界的区域全含于 互不包含也互不相交并且以 是 在 内部的简单闭曲线它 们 设 为多连通域 内的一条简单闭曲线 如果 f (z)在 D内解析, D C C1 C2 C3 那末 (1) ( )d ( )d , 1 = = n k C C k f z z f z z 其中 及 均取正方向; C Ck