
第五章第四节定积分的应用一、微元法定积分在几何上的应用1、平面图形的面积2、体积3、平面曲线的弧长HIGH EDUCATION PRESS
第四节 定积分的应用 一、微元法 第五章 二、定积分在几何上的应用 1、平面图形的面积 2、体积 3、平面曲线的弧长
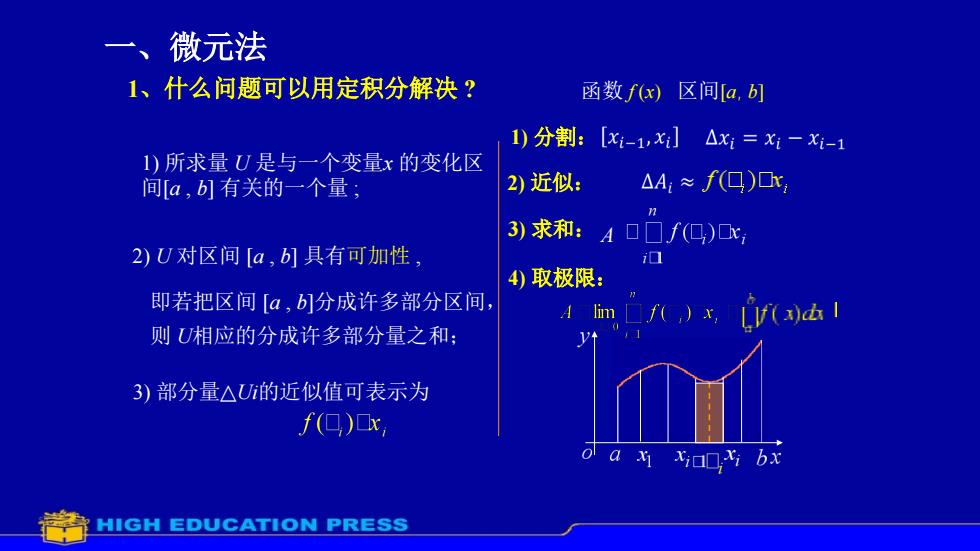
一、微元法1、什么问题可以用定积分解决?函数f(x)区间[a,b]1)分割: [xi-1,xi] △xi = xi - xi-11)所求量U是与一个变量x的变化区AA, ~ f()x2)近似:间[a,b]有关的一个量;3)求和:Af()x2U对区间[a,b]具有可加性04)取极限:即若把区间「a,b1分成许多部分区间LV(a)d!Alimf() x则U相应的分成许多部分量之和:际V3)部分量△Ui的近似值可表示为f(o)x0axixianx;bxHIGH EDUCATION PRESS
1、什么问题可以用定积分解决 ? 1) 所求量 U 是与一个变量x 的变化区 间[a , b] 有关的一个量 ; 2) U 对区间 [a , b] 具有可加性 , 即若把区间 [a , b]分成许多部分区间, 则 U相应的分成许多部分量之和; 3) 部分量△Ui的近似值可表示为 1) 分割: 2) 近似: 3) 求和: 4) 取极限: 函数 f (x) 区间[a, b] A 一、微元法

2、如何应用定积分解决问题?第一步根据问题的具体情况,选取一个变量(例如x)为积分变量,并确定它的变化区间[a,b];0xx口dxa第二步写出所求量的元素dU口f(x)dxbx设想把区间[a,b]分成n个小区间,取其中任意一小区间并记作[x,x+dx],求出相应于这个小区间的部分量△U的近似值f(x)dx;)第三步写出所求量的积分表达式 UCf(x)dx这种分析方法成为元素法(或微元法)元素的几何形状常取为:条,带,段,环,扇,片等HIGH EDUCATION PRESS
第一步 根据问题的具体情况,选取一个变量(例如 x) 为积分变量, 这种分析方法成为元素法 (或微元法) 元素的几何形状常取为: 条, 带, 段, 环, 扇, 片 等 并确定它的变化区间[a, b]; 第二步 写出所求量的元素 {设想把区间[a, b]分成n个小区间,取其中任意一小区间 并记作[x, x+dx] ,求出相应于这个小区间的部分量△U 的近似值 ;} 2 、如何应用定积分解决问题 ? 第三步 写出所求量的积分表达式
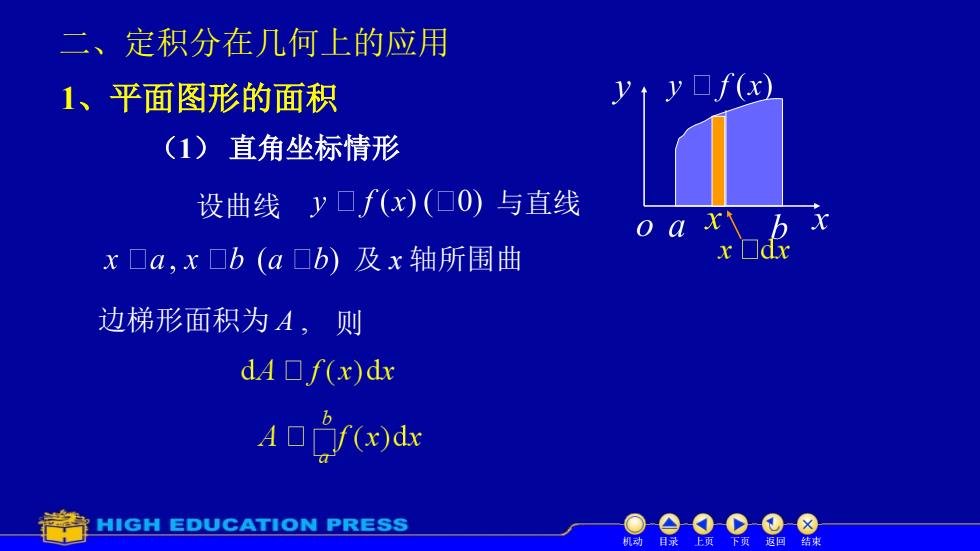
二、定积分在几何上的应用yt yf(x)1、平面图形的面积直角坐标情形(1设曲线口f(x)(O)与直线xlbxoadxxa,xb(ab)及x轴所围曲边梯形面积为A,则dAf(x)dxA f(x)dxHIGH EDUCATION PRESS日医店
1、平面图形的面积 (1) 直角坐标情形 设曲线 与直线 及 x 轴所围曲 则 机动 目录 上页 下页 返回 结束 边梯形面积为 A , 二、定积分在几何上的应用

例1.计算两条抛物线2x,yx2在第一象限所围所围图形的面积xy? x a,1)解:由得交点(0,0),(1,1)y口x2中x取横坐标x为积分变量,它的变化区间[0,1],xIdx相应于[0,1]上的任一小区间[x,x+dx]X的窄条面积近似于高为口x2[底为dx的窄矩形的面积,即得面积元素为 dAx?axAxaxxHIGH EDUCATION PRESS
相应于[0,1]上的任一小区间[x, x+dx] 的窄条面积近似于 在第一象限所围 所围图形的面积 . 解: 由 得交点 机动 目录 上页 下页 返回 结束 例1. 计算两条抛物线 取横坐标x为积分变量,它的变化 区间[0,1]. 的窄矩形的面积,即得面积元素为