《高等数学》课程教学资源（课件讲稿）第3章 第6讲 弧微分与曲率

高等数学（上册）第3章微分中值定理与导数的应用第6讲弧微分与曲率人民邮电出版社POSIS&TELECOMPRESS

高等数学（上册） 第6讲 弧微分与曲率 第3章 微分中值定理与导数的应用

R人邮教育本讲内容w.ryjiaoyu.co弧微分曲率0203曲率半径与曲率圆

01 弧微分 02 曲率 03 曲率半径与曲率圆 本 讲 内 容

01弧微分CO0R人邮教育定义曲线y=f(x)上的弧值函数s=s(x)设y=f(x)在(a,b)内有连续导数，y =f(x)M。（xoyo）作为度量弧长的基点，MMo规定：x增大的方向为正向*x

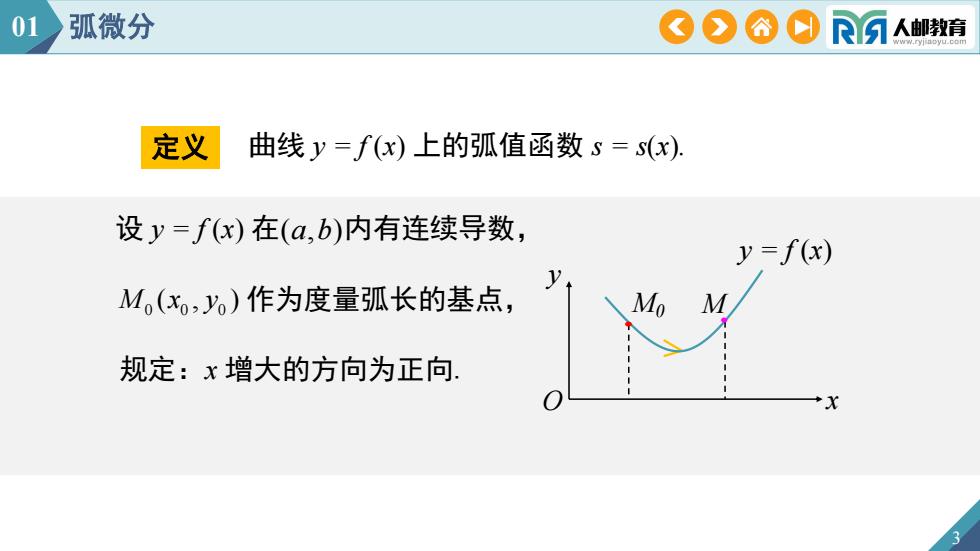
定义 3 曲线 y = f (x) 上的弧值函数 s = s(x). 设 y = f (x) 在(a,b)内有连续导数， M0 (x0 , y0 ) 作为度量弧长的基点， 规定：x 增大的方向为正向. y O x  y = f (x) M0 M  01 弧微分

01弧微分OOOORA人邮教育对曲线上任意一点M(x，y)，规定有向弧段MM的值s：①s的绝对值为弧段的长度；②当方向与曲线的正向一致时，s>0；③当方向与曲线的正向相反时，s<0，显然，s是x的函数s=s(x)，且单调增加，y=f(x)yMoMC+x

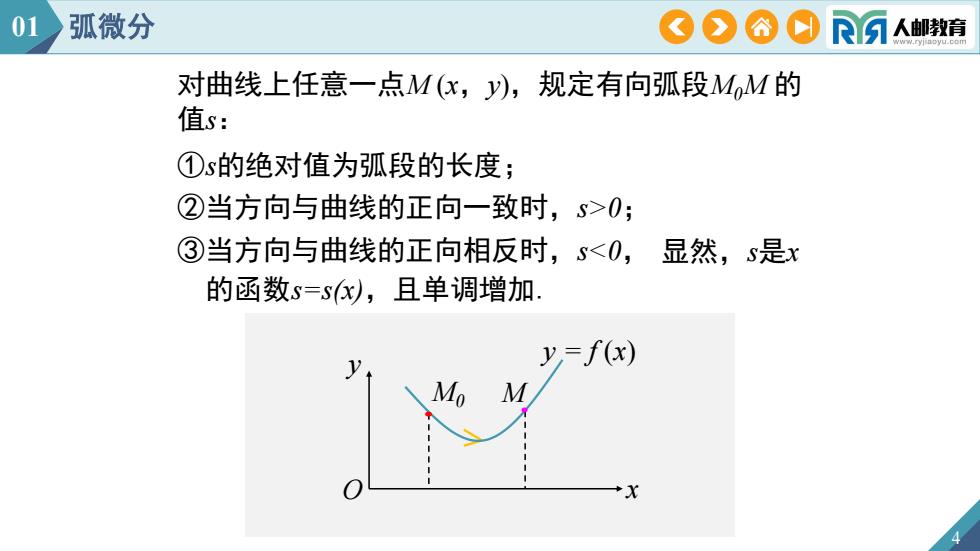
4 对曲线上任意一点M (x，y)，规定有向弧段M0M 的 值s： ①s的绝对值为弧段的长度； ②当方向与曲线的正向一致时，s>0； ③当方向与曲线的正向相反时，s<0， 显然，s是x 的函数s=s(x)，且单调增加. y O x  y = f (x) M0 M  01 弧微分

01弧微分COAO人邮教育RAds△slimds = s(x)dx先求s=s(x)的导数弧微分公式ds=？dxAr-→0 △xAs=?Ax在x处给自变量x一增量△x，Mf(x)yI=MoAy相应的有向弧段的值s有增量MAs ,Ar△s= s(x+△x)-s(x)--0x-x+Ax xXo=M.M-M.M =MMAsAsMMMMMM'AxAxAxMM"Ar△s与△x总是同号的

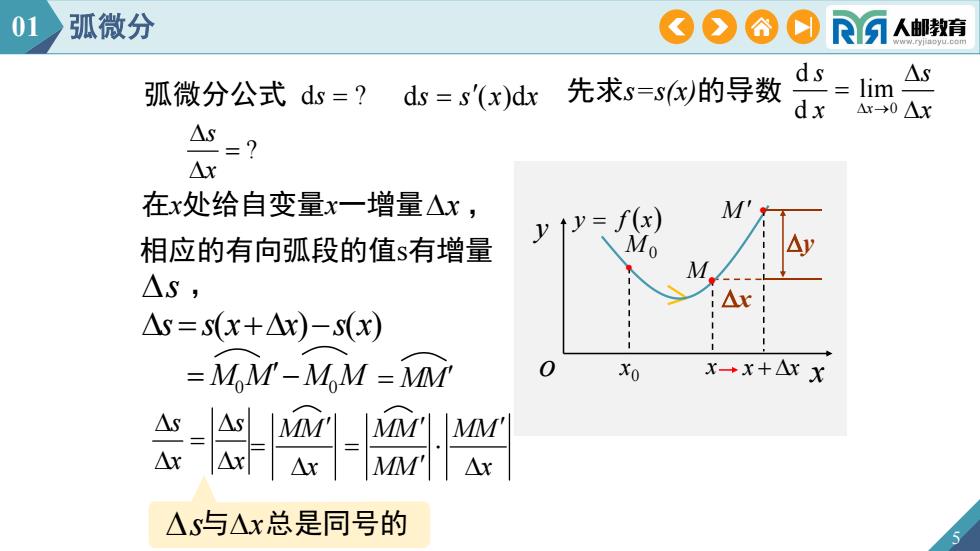
ds  s (x)dx ? s x    0 0  M MM M  MM s s x x      MM x    5 先求s=s(x)的导数 0 d lim d x s s x   x    在x处给自变量x一增量x ， s与x总是同号的 M0 M M   y x y  f x   相应的有向弧段的值s有增量 s ， 弧微分公式 ds  ? 0 o x x x  x x y MM MM MM x       01 弧微分 s s(xx)s(x)