
第一章第五节两个重要极限夹逼准则及第一重要极限单调有界收敛准则及第二重要极限HIGH EDUCATION PRESS目录上页下页返回机动结束
二、 单调有界收敛准则及第二重要极限 一、 夹逼准则及第一重要极限 第五节 机动 目录 上页 下页 返回 结束 两个重要极限 第一章

夹逼准则一、准则I.如果数列满足下列条件:(xn)(yn)(zn)(1)从某项起,即EnEN当n>n时,≤X≤z(2) lim y, =a,lim z, = an-0n-0limx, =a那么数列(x)的极限存在,且n-8HIGHEDUCATION PRESS
n n n y x z 0 0 n N n n + 当 时, (2 lim , lim ) n n n n y a z a → → = = 准则I. 如果数列 满足下列条件: (1)从某项起,即 那么数列 的极限存在,且 一、 夹逼准则 x y z n n n 、 、 xn lim n n x a → =

准则r.如果函数 f(x),g(x),h(x)满足下列条件()当xeU(x,)时, g(x)≤ f(x)≤h(x)(2) lim g(x) = lim h(x) = AX-→XoX→xo那么 lim f(x)存在,且 lim n f(x)=AX→X0x-→XoHIGHEDUCATION PRESS机动目录上页下页返回结束
( ) 0 1 ( , ) , 当 x x 时 ( ) 0 0 2 lim ( ) lim ( ) x x x x g x h x A → → = = g(x) f (x) h(x) , f x A x x = → lim ( ) 0 机动 目录 上页 下页 返回 结束 准则I`. 如果函数 f x g x h x ( ) ( ) ( ) , , 满足下列条件: 那么 存在,且 0 lim ( ) x x f x →
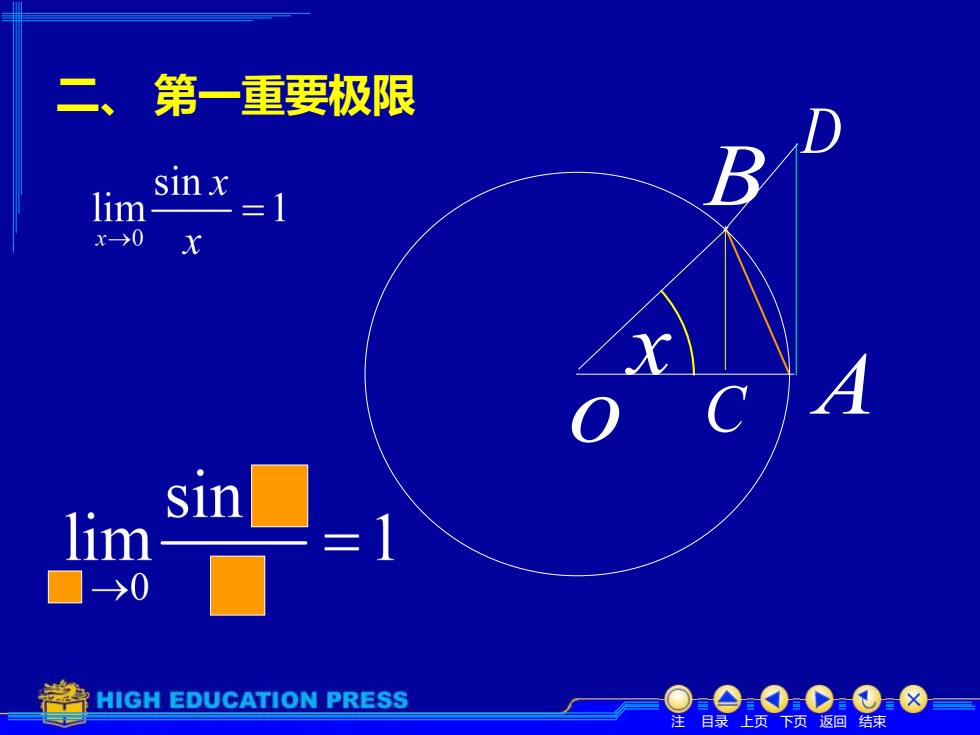
二、第一重要极限TBsinxlimX-0xxAC0sin=1lim-0HIGHEDUCATION PRESS目录上页返回结束注下页
D C B A x o 注 目录 上页 下页 返回 结束 二、 第一重要极限

sin xlimlim xsinx-0xx-0sinxlimxsin1mx00XX0xHIGH EDUCATION PRESS第七节目录上页结束下页返回
sin lim _ x x → x = 1 lim sin _ x x → x = 0 1 lim sin _ x x → x = 0 sin lim _ x x → x = 0 1 0 第七节 目录 上页 下页 返回 结束 1