
第一章第二节函数极限的定义自变量趋于无穷大时函数的极限一、目二、自变量趋于有限值时函数的极限函数极限的性质一、HIGHEDUCATIONPRESS机动目录上页下页返回结束
第一章 二、自变量趋于有限值时函数的极限 第二节 一、自变量趋于无穷大时函数的极限 机动 目录 上页 下页 返回 结束 函数极限的定义 三、函数极限的性质
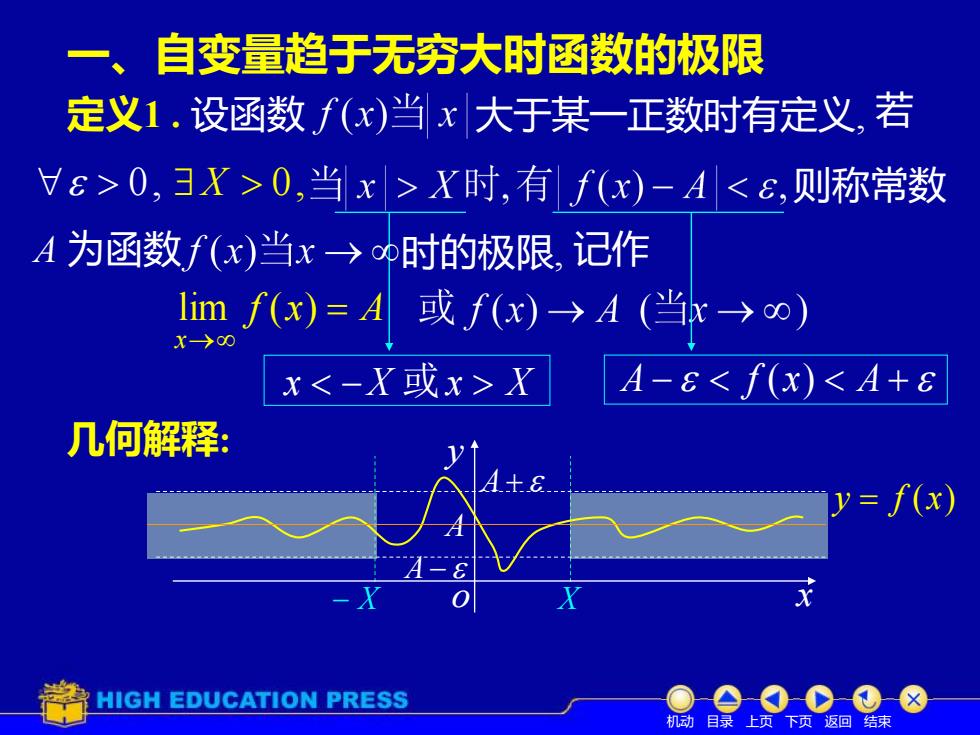
一、目自变量趋于无穷大时函数的极限定义1.设函数f(x)当x|大于某一正数时有定义,若>0,X>0,当 x|>X时,有f(x)-A<ε,则称常数A 为函数f(x)当x→αp时的极限,记作lim f(x) = A或f(x)→A (当x→)X→80A-ε<f(x)<A+x<-X或x>X几何解释:Atay= f(x)0XHIGH EDUCATION PRESS机动目录上页下页返回结束
− X X A + A − o x y y = f (x) A 一、自变量趋于无穷大时函数的极限 定义1 . 设函数 大于某一正数时有定义, 若 X 0, 则称常数 时的极限, f x A x = → lim ( ) 几何解释: x −X 或x X A − f (x) A + 记作 0, 机动 目录 上页 下页 返回 结束 A 为函数
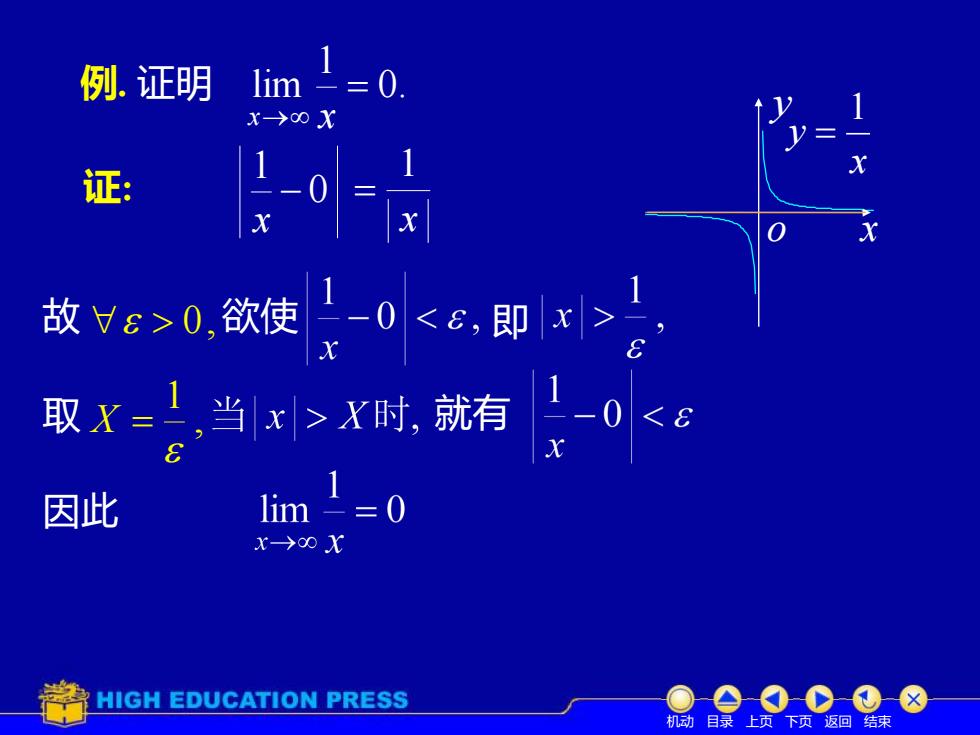
例.证明limx-00 xX证:故ε>0,欲使<ε,即x取X==,当|x|>X时,就有CX因此limx→0 xHIGH EDUCATION PRESS机动目录上页下页返回结束
例. 证明 0. 1 lim = x→ x 证: 0 1 − x x 1 = 取 , 1 X = 因此 就有 故 0, 欲使 即 o x y x y 1 = 机动 目录 上页 下页 返回 结束

两种特殊情况:lim f(x)=Aε>0,3X>0,当 x>X时,有x→+00f(x)-A<lim f(x)=AV>0,X>0,当x<-X时,有x-00f(x)-A<8lim f(x)= A= lim f(x)lim f(x)= Ax→-8X→+80x0HIGH EDUCATION PRESS机动目录上页下页返回结束
两种特殊情况 : f x A x = →+ lim ( ) 0, X 0, 当 时, 有 f (x) − A 0, X 0, 当 x −X 时, 有 f (x) − A 机动 目录 上页 下页 返回 结束 lim ( ) lim ( ) x x f x A f x →− →+ = =
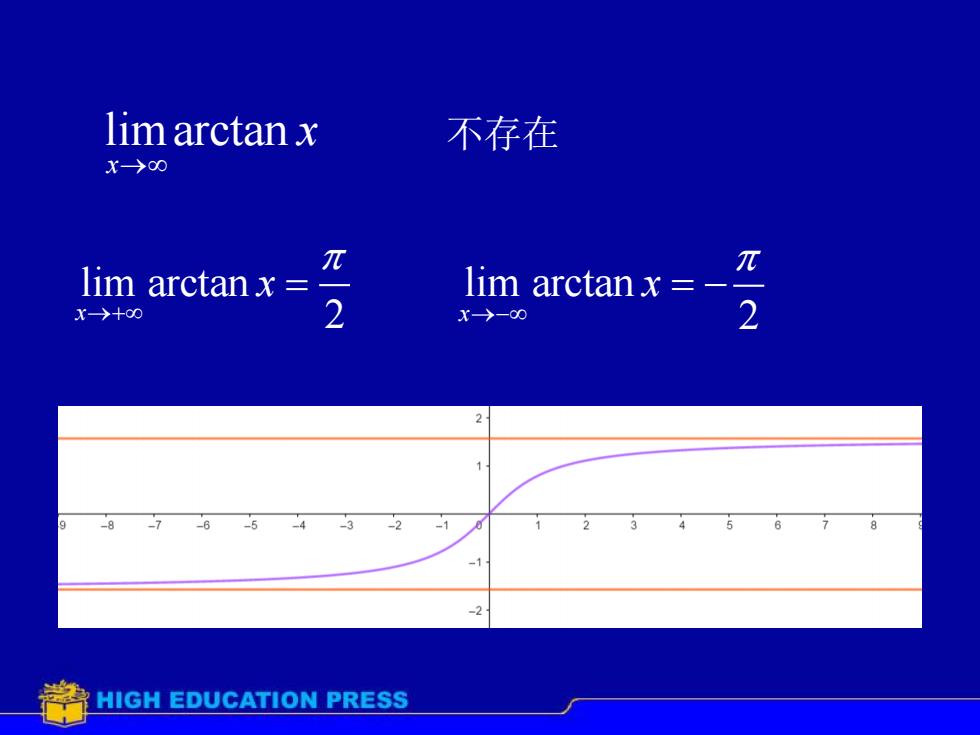
lim arctan x不存在x-8元元lim arctan x :lim arctan x =22x→+o0X→-0-6-5-4-3-256-74-8-13HIGH EDUCATION PRESS
limarctan x x → lim arctan x 2 x →− lim arctan = − x 2 x →+ = 不存在