
高等数学(上册)第3章微分中值定理与导数的应用第5讲曲线的凹凸性及函数作图人民邮电出版社POSTS&TELECOMPRESS
高等数学(上册) 第5讲 曲线的凹凸性及函数作图 第3章 微分中值定理与导数的应用

R人邮教育本讲内容nw.ryjinoyu.c01曲线的凹凸性与拐点02曲线的渐近线03函数作图
01 曲线的凹凸性与拐点 02 曲线的渐近线 03 函数作图 本 讲 内 容
01OOAOR曲线的凹凸性与拐点人邮教育定义3.2设函数f(x)在区间/上连续,对I上任意两点x,和x2f(x)+ f(x2)aexi+x,o总有厂则称在区间I上的图形是凹Ce220的,如下图;f(x,+X2if (x2L2XIX2x
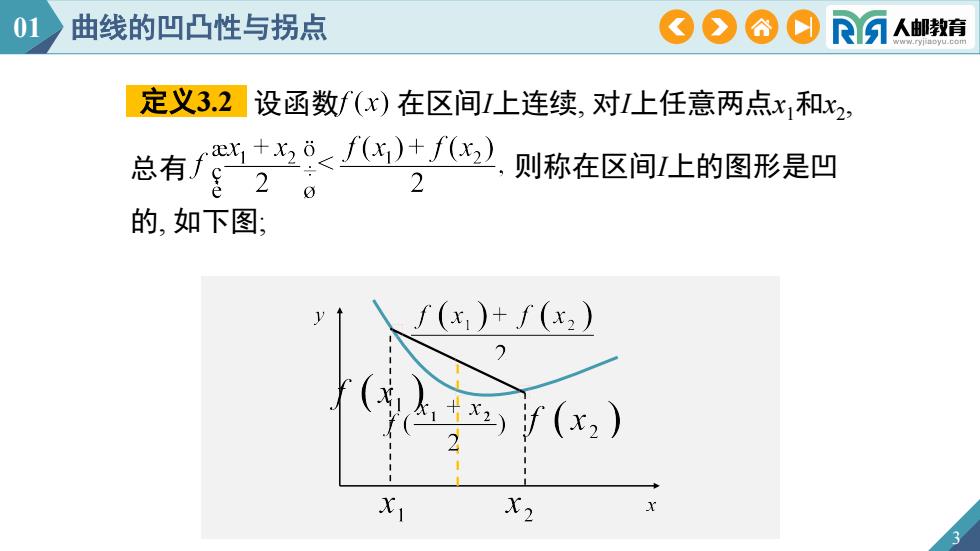
设函数 在区间I上连续, 对I上任意两点x1和x2 定义3.2 , 3 总有 则称在区间I上的图形是凹 的, 如下图; 01 曲线的凹凸性与拐点

01曲线的凹凸性与拐点COA0RA人邮教育f(x)+ f(x2)ax+x,o若总有ce220则称在区间I上的图形是凸的,如下图F(+x21.2(X)(x,万xif(x)xX1X2
4 若总有 则称在区间I上的图形是凸的, 如下图. 01 曲线的凹凸性与拐点

01C0曲线的凹凸性与拐点RA人邮教育定义3.3连续曲线上凹凸区间的分界点,称为曲线的拐点注:(1)拐点是曲线上的点,应以坐标点(xo,f(x))表示(2)注意与极值点x=x.表示形式的不同
(1)拐点是曲线上的点, 应以坐标点 表示. (2)注意与极值点 表示形式的不同. 5 定义3.3 连续曲线上凹凸区间的分界点, 称为曲线的拐点. 注: 01 曲线的凹凸性与拐点