
第五章第四节反常积分无穷区间上的反常积分一二、天无界函数的反常积分HIGH EDUCATION PRESS机动目录上页下页返回结束
二、无界函数的反常积分 第四节 一、无穷区间上的反常积分 机动 目录 上页 下页 返回 结束 反常积分 第五章
无穷区间上的反常积分一、引例.曲线和直线x=1及x轴所围成的开口曲V=边梯形的面积可记作A=WdxblimA=limJb-→+8b-→+limb→+ooHIGH EDUCATION PRESS机动目录上页下页返回结束
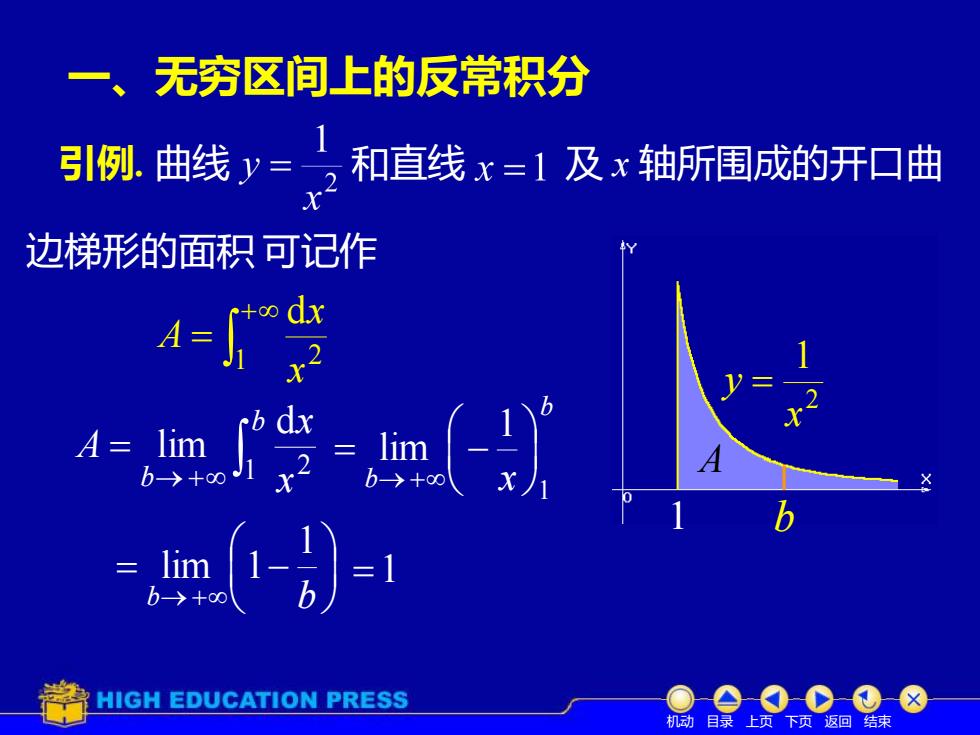
一、无穷区间上的反常积分 引例. 曲线 和直线 及 x 轴所围成的开口曲 边梯形的面积 2 1 x y = A 1 可记作 + = 1 2 d x x A → + = b b x x A 1 2 d lim b b b x 1 1 lim = − →+ = − b→+ b 1 lim 1 =1 机动 目录 上页 下页 返回 结束

定义l.设 f(x)eC[a,+),取b>a,若rblim. f(x)dxb→+oJa记作存在,则称此极限为f(x)的无穷限反常积分.b+8f(x)dx = lim(f(x)dxb-→+Ja+8这时称反常积分f(x)dx收敛;如果上述极限不存在a+8f(x)dx发散就称反常积分Ja类似地,若 f(x)EC(-o,b],则定义brbf(x)dx = lim/f(x)dxa-aHIGH EDUCATIONPRESS机动目录上页下页返回结束
定义1. 设 f (x)C[a, + ), 取b a, 若 存在 , 则称此极限为 f (x) 的无穷限反常积分, 记作 这时称反常积分 收敛 ; 如果上述极限不存在, 就称反常积分 发散 . 类似地 , 若 f (x)C (−, b], 则定义 机动 目录 上页 下页 返回 结束

若 f(x)EC(-80,+),则定义F-f(x)dx + limf(x)dxf(x)dx = limb→+oo Jca-8a(c为任意取定的常数)-只要有一个极限不存在,就称f(x)dx 发散HIGH EDUCATION PRESS机动目录上页下页返回结束
若 f (x)C (−, + ), 则定义 f x x c a a lim ( )d →− f x x b b c lim ( )d →+ + ( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 发散 . 机动 目录 上页 下页 返回 结束

若F(x)是f(x)的原函数,引入记号F(+oo)= lim F(x); F(-oo)= lim F(x)x→+8x→-8则有类似牛一莱公式的计算表达式+8= F(+o)- F(a)f(x)dx= F(x)Chf(x)dx = F(x)= F(b)- F(-00)18+8 f(x)dx = F(x)= F(+8)- F(-8)-8HIGH EDUCATION PRESS机动目录上页下页返回结束
引入记号 F( ) lim F(x) ; x→+ + = F( ) lim F(x) x→− − = 则有类似牛 – 莱公式的计算表达式 : f x x a ( )d + = F(x) = F(+) − F(a) f x x b ( )d − = F(x) = F(b) − F(−) f (x)dx + − = F(x) = F(+) − F(−) 机动 目录 上页 下页 返回 结束