
在二次型的矩阵表示中,任给一个二次型,就唯 一确定一个对称矩阵;反之,任给一个对称矩阵, 也可唯一确定一个二次型.这样,二次型与对称 矩阵之间存在一一对应的关系. 定义2:二次型f=x'x 把对称矩阵A称为二次型∫的矩阵, 也把二次型f称为对称矩阵A的二次型, 对称矩阵A的秩称为二次型∫的秩
在二次型的矩阵表示中,任给一个二次型,就唯 一确定一个对称矩阵;反之,任给一个对称矩阵, 也可唯一确定一个二次型.这样,二次型与对称 矩阵之间存在一一对应的关系. 把对称矩阵 A 称为二次型 f 的矩阵, 也把二次型 f 称为对称矩阵 A 的二次型, 对称矩阵 A 的秩称为二次型f 的秩. T 定义2:二次型 f x Ax =

例1:求二次型f的矩阵 f(x,2,x3,x4)=+2x☑+7x2.xx22x 4x34 A= 2 0 0 0 2 0 0 27
例1:求二次型 f 的矩阵 222 1 2 3 4 1 2 4 1 2 2 3 3 4 f x x x x x x x x x x x x x ( , , , ) 2 7 2 2 4 = + + − − + 1 1 0 0 1 2 1 0 0 1 0 2 0 0 2 7 A − − − = −
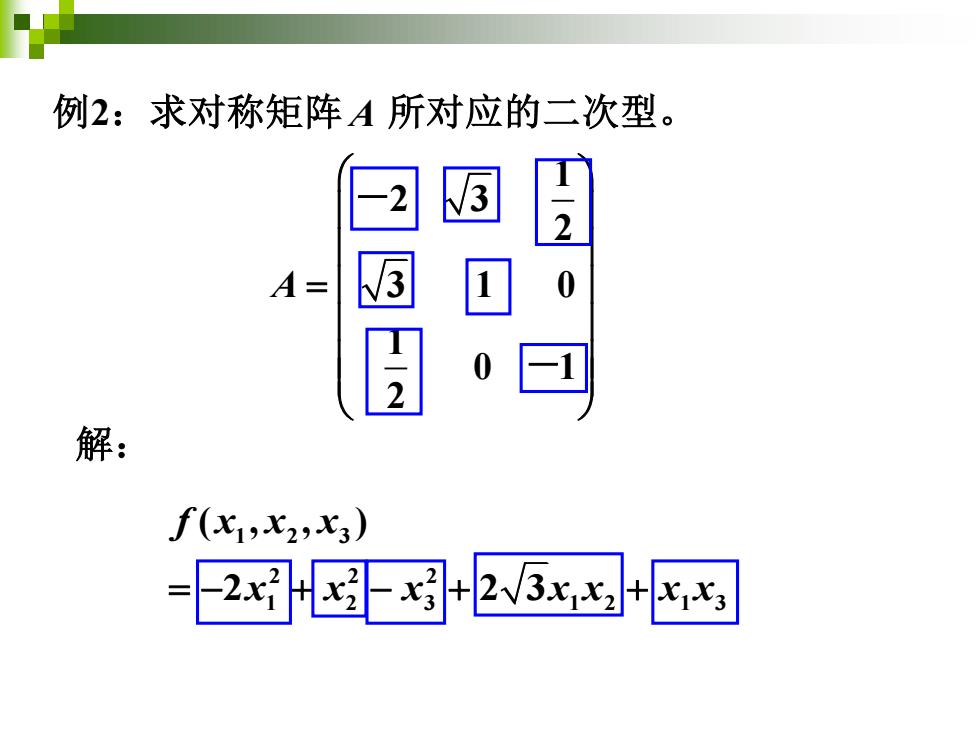
例2:求对称矩阵A所对应的二次型。 3 A= 0 2 解: f(X1,x2,x3) =2x网+23xx xX3
1 2 3 2 3 1 0 1 0 1 2 A = - - 例2:求对称矩阵 A 所对应的二次型。 1 2 3 2 2 2 1 2 3 1 2 1 3 ( , , ) 2 2 3 f x x x = − + − + + x x x x x x x 解:

例3:已知二次型f的秩为2,求参数c。 f(x1,x2,x3)=5x+5x3+cx5-2xK2+6xK3-6x2 解: 5 -1 3 A= -1 3 33 QR(A)=2 ∴.A=0 →C=3
Q R A( ) 2 = 例3:已知二次型 的秩为2,求参数c。 2 2 2 1 2 3 1 2 3 1 2 1 3 2 3 f x x x x x cx x x x x x x ( , , ) 5 5 2 6 6 = + + − + − f 5 1 3 1 5 3 3 3 A c − = − − − 解: = 0 A = c 3