
实二次型:,为实数。(我们仅讨论实二次型) 复二次型:,为复数。 例如:f(x,y)=x2+4y+5y2 f(x,y,z)=2x2+y2+xz+yz 都是二次型。 f(x1,x2,3)七4)=x1x2+x2x3+x2x4 f(x,y)=x2+y2+5 f(x,y)=2x2-y2+2x }不是次
实二次型: aij 为实数。(我们仅讨论实二次型) 复二次型: aij 为复数。 例如: 2 2 f x y x xy y ( , ) 4 5 = + + 2 2 f x y z x y xz yz ( , , ) 2 = + + + 1 2 3 4 1 2 2 3 2 4 f x x x x x x x x x x ( , , , ) = + + 都是二次型。 2 2 f x y x y ( , ) 5 = + + 2 2 f x y x y x ( , ) 2 2 = − + 不是二次型

只含有平方项的二次型f=ky+k2y经+.+kn 称为二次型的标准形。 例如:f(x1,2,x)=2x+4x号+5x号-4xK3 f(x1,2,3)=2+Xx3+x23 都为二次型; f(1,x2,K3)=x+4x3+4x 为二次型的标准形
只含有平方项的二次型 2 2 2 2 2 1 1 n n f = k y + k y ++ k y 称为二次型的标准形。 例如: ( ) 1 3 2 3 2 2 2 1 2 3 1 f x , x , x = 2x + 4x + 5x − 4x x 都为二次型; ( ) 2 3 2 2 2 1 2 3 1 f x , x , x = x + 4x + 4x 为二次型的标准形。 ( ) 1 2 3 1 2 1 3 2 3 f x , x , x = x x + x x + x x

取0=0 则2ag火j=xx;+anX:Xj 则(1)式可以表示为 f=auxi+anx:x2+L+aunxxn +21X2X1+22x号+L+2m2n +① 二次型用和号表示 +5+a5t+a=a =X,(a111+012X2+L+41mn) +X2(a21X1+22X2+L+42mXn) +L +x(amx1+an2x2+L amnx)
2 2 11 12 2 1 1 2 1 21 1 22 2 1 1 2 2 2 2 1 2 n n n n n n nn n n n f a a x a x a x a x x a x x x x a a a x x x x x = + + + x + + + + + + + + + L L L L ij ji 取 a a = 2 ij i j ij i j ji i j 则 a x x a x x a x x = + 则(1)式可以表示为 1 11 1 12 2 1 ( ) n n = + + + x a x a x x L a 2 21 1 22 2 2 ( ) n n + + + + x a x a x x L a +L 1 1 2 2 ( ) n n n nn n + + + + x a x a x L a x , 1 n ij i j i j a x x = = 二次型用和号表示

411七1+012x2+L+41nXn az1x1+a22x2+L+aznx =(x1,x2,L,xn) M amx1+an2x2+L+amnxn 12 L 21 l22 L =(X13X2,L,Xn) Q2n 七 M M L x
11 1 12 2 1 21 1 22 2 2 1 2 1 1 2 2 ( , , , ) n n n n n n n nn n a x a x a x a x a x a x x x x a x a x a x + + + + + + = + + + L L L M L 11 12 1 1 21 22 2 2 1 2 1 2 ( , , , ) n n n n n nn n a a a x a a a x x x x a a a x = L L L M M L
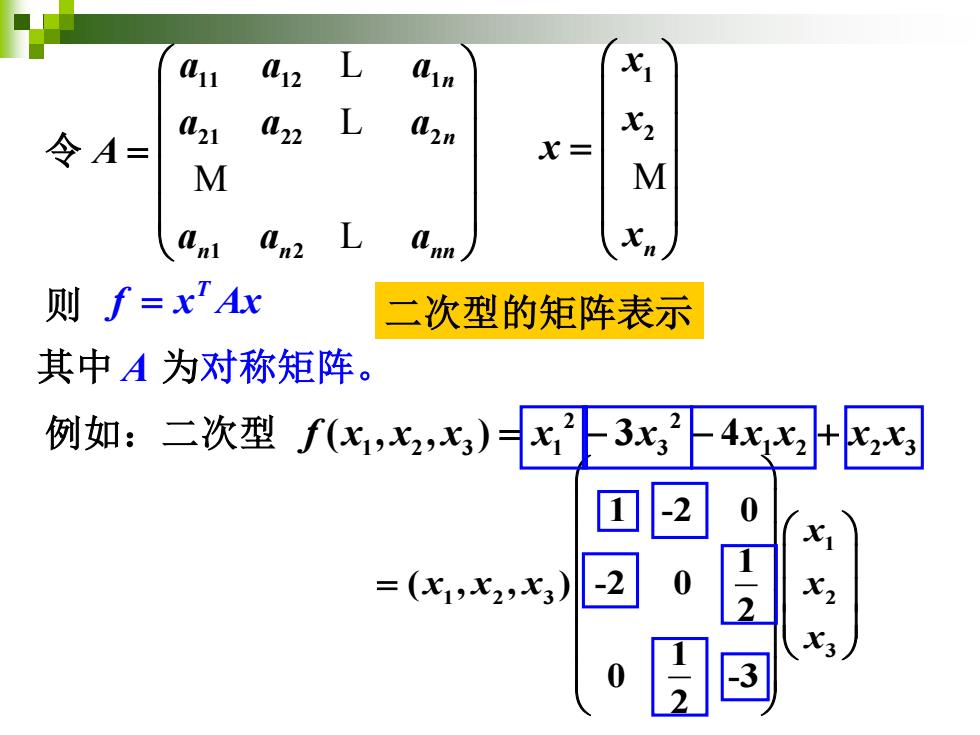
11 L12 L Qin X1 令A= 21 42 L Q2n X= M M An An2 L 则f=x'Ax 二次型的矩阵表示 其中A为对称矩阵。 例如:二次型f(x,七,)x3x,2 4 回-2 0 =(x1,X2,x3) 2
1 2 n x x x x = M 11 12 1 21 22 2 1 2 n n n n nn a a a a a a A a a a = L L M L 令 T 则 f x Ax = 其中 A 为对称矩阵。 二次型的矩阵表示 1 1 2 3 2 3 1 -2 0 1 ( , , ) -2 0 2 1 0 -3 2 x x x x x x = 2 2 1 2 3 1 3 1 2 2 3 例如:二次型 ( , , ) 3 4 f x x x x x x x x x = − − +