
第二节向量及其线性运算

1.向量的概念 定义2.2.1:n个有次序的数41,a2,L,4n所组成的有序数组 (a1,a2,4n)称为一个n维向量。 这n个数称为该向量的n个分量,第个数a 称为第个分量(坐标)。 分量全为实数的向量称为实向量, 以后我们用小写希腊字母,b8L来代表向量
分量全为实数的向量称为实向量, 1. 向量的概念 定义2.2.1:n 个有次序的数 所组成的有序数组 称为一个n 维向量。 这 n 个数称为该向量的 n 个分量,第 个数 称为第 个分量(坐标)。 以后我们用小写希腊字母 来代表向量
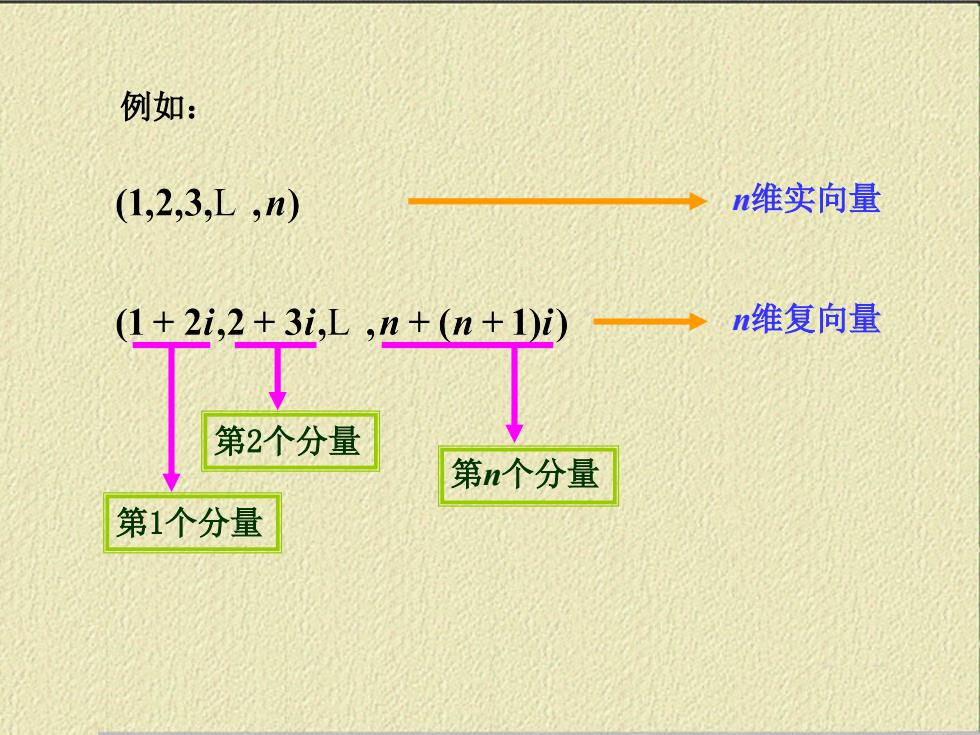
例如: (1,2,3,L,n) →n维实向量 (1+2i,2+3i,L,n+(n+1)) →n维复向量 第n个分量 第1个分量
例如: n维实向量 n维复向量 第1个分量 第n个分量 第2个分量

向量通常写成一行:0=(a1,42,L,an) 称为行向量。 28m10 有时也写成一列:a=S。 S 称为列向量。 它们的区别 只是写法上 ca 的不同。 分量全为零的向量(0,0,L,0)称为零向量。 2.向量的运算和性质 向量相等:如果n维向量4=(a1,a2,L,4n) b=(b,b2,L,b 的对应分量都相等,即4,=b(i=1,2,L,n) 就称这两个向量相等,记为a=b
向量通常写成一行: 有时也写成一列: 称为行向量。 称为列向量。 它们的区别 只是写法上 的不同。 分量全为零的向量 称为零向量。 2. 向量的运算和性质 向量相等:如果 n 维向量 的对应分量都相等,即 就称这两个向量相等,记为

向量加法:向量8=(a1+b,a2+b2,L,4n+bn) 称为向量a=(41,42,L,4n) b=(B,bL,b) 的和,记为g=4+b 负向量:向量a=((a1,-2,L,-4n)称为向量a的负向量 向量减法:a-b=a+(-b) 数乘向量:设k为数域P中的数,向量(ka1,ka2,L,kan) 称为向量a=(a1,a2,L,an) 与数k的数量乘积。记为k@
向量加法:向量 称为向量 的和,记为 负向量:向量 称为向量 的负向量 向量减法: 称为向量 与数k的数量乘积。记为