西安电子科技大学：《矩阵论》课程教学资源（电子讲义）第五讲 对角化与Jordan标准形

H H H 1414u2 …un H H H U"U。= [4…n] =In 412…44n 对A进行酉相似变换： 4 UNAU= A[4h2…4n]=(gAu) 6

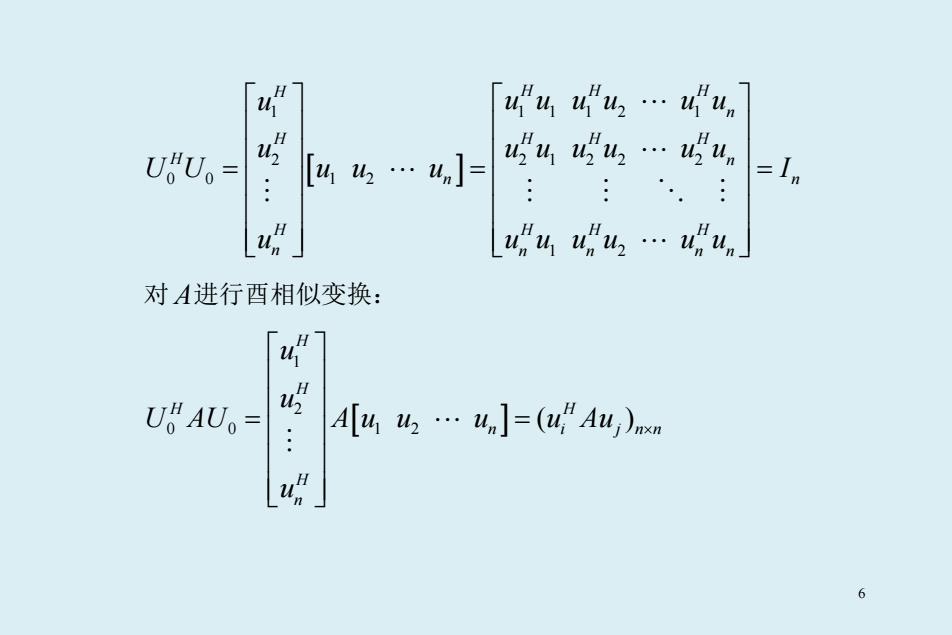
[ ] 1 11 12 1 2 21 22 2 0 0 1 2 1 2 H HH H n H HH H H n n n H HH H n n n nn u uu uu uu u uu uu uu UU uu u I u uu uu uu           = = =                   对 A进行酉相似变换： [ ] 1 2 0 0 1 2 ( ) H H H H n i j nn H n u u U AU A u u u u Au u ×       = =           6

i≠1 第一列：4A叫=4元4=元44=2 i=1 * … .H HAun (4)n-1n-)= A[44…4]= A…A, un 7

第一列： HH H 1 11 1 1 1 0 1 1 ii i i u Au u u u u i  ≠ = = =   = λ λ λ 0 0 1 ( 1) ( 1) 0 ( ) 0 H n n U AU A λ −× −   ∗   =    [ ] 2 22 2 3 1 ( 1)( 1) 2 3 2 ( ) H H H H n n n n H H n n n H n u u Au u u u A Au u u u Au u u u − −           = =           A A      7

相似矩阵具有相同的特征值，因此，对于A,其特征值为入2，…，入n, 与上相同，可得一个酉矩阵U,使得 米 0 URAU= (4a-2n-a 10 依次类推，分别可找到西矩阵U2,U3,…,Un2使 8

相似矩阵具有相同的特征值，因此，对于 A1，其特征值为 2 , , λ λ  n， 与上相同，可得一个酉矩阵U1，使得 2 1 11 2 ( 2) ( 2) 0 ( ) 0 H n n U AU A λ −×−   ∗   =    依次类推，分别可找到酉矩阵 23 2 , ,, UU U  n− 使 8

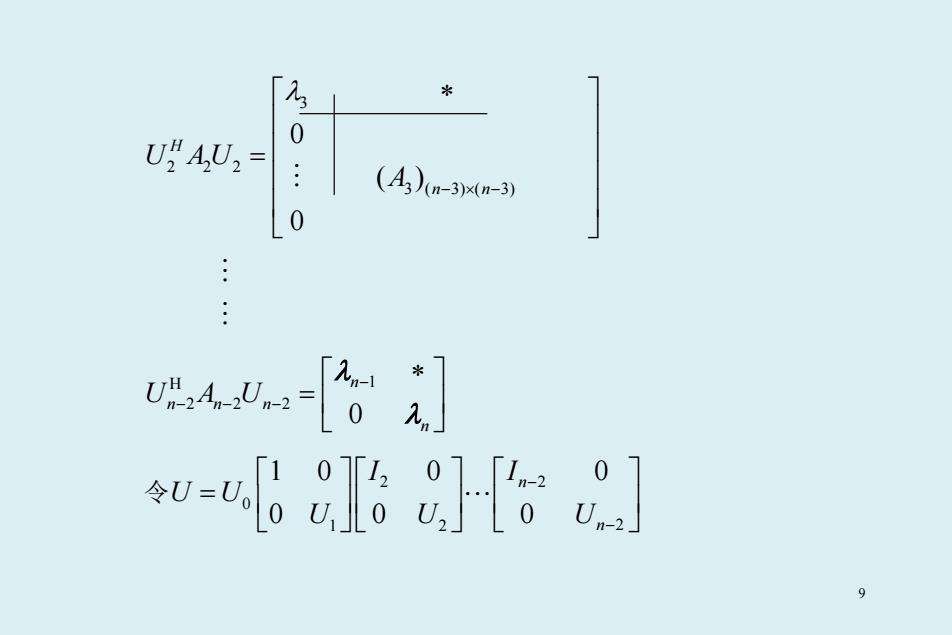
米 0 U"AU2 . (4,)n-3m-3 10 : =b60[e] 9

3 2 22 3 ( 3) ( 3) 0 ( ) 0 H n n U AU A λ −×−   ∗   =     H 1 22 2 0n nn n n U AU − −− −   ∗ =     λ λ 令 2 2 0 1 2 2 10 0 0 0 0 0n n I I U U U U U − −      =            9

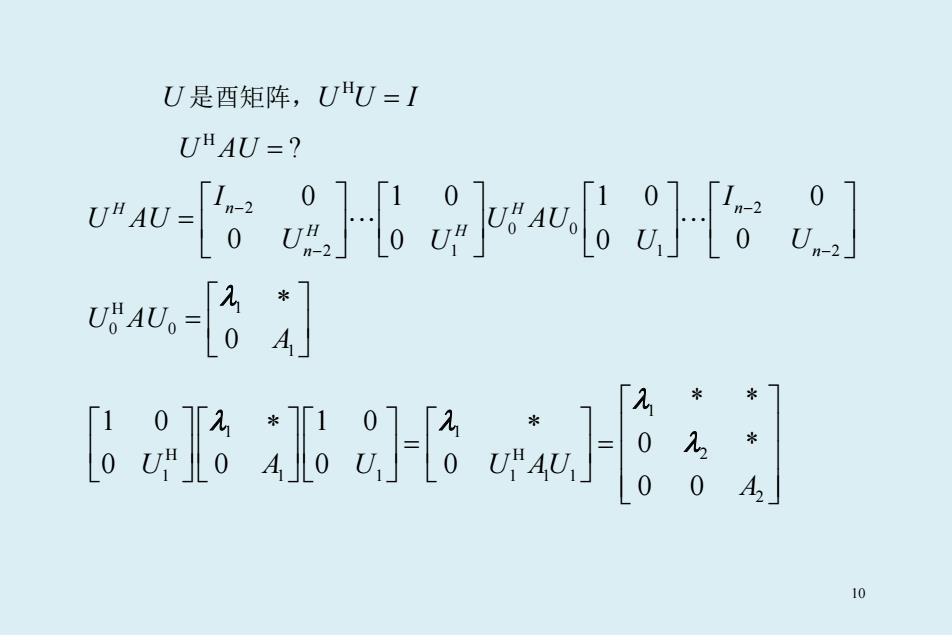
U是酉矩阵，UU=I UHAU=? waw-g0ab。] 4-[百 b 63 A 10

U 是酉矩阵， H UU I = H U AU = ? 2 2 0 0 2 2 1 1 0 0 1 0 10 0 0 0 0 H H n n H H n n I I U AU U AU U U U U − − − −        =                 H 1 0 0 1 0 U AU A   ∗ =     λ 1 1 1 H H 2 1 1 1 1 11 2 * * 1 0 10 0 * 0 00 0 0 0 U A U U AU A         ∗ ∗   = =                   λ λ λ λ 10