
第十一讲矩阵的QR分解
第十一讲 矩阵的 QR 分解 1
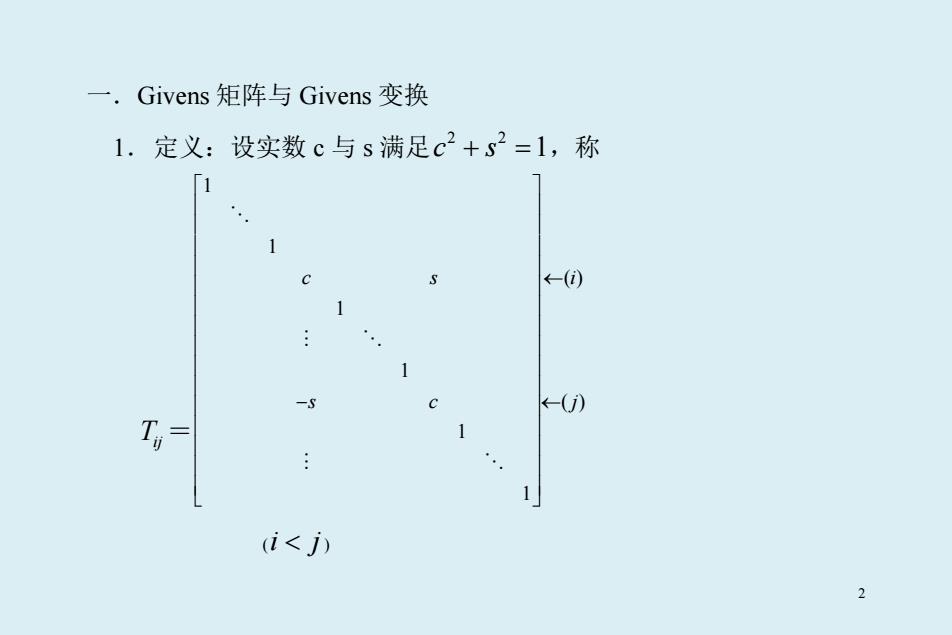
一.Givens矩阵与Givens变换 1.定义:设实数c与s满足c2+s2=1,称 S ←-() 1 -s ←-() T = 1 1 (i<j) 2
一.Givens 矩阵与 Givens 变换 1.定义:设实数 c 与 s 满足 2 2 c s + = 1,称 Tij = 1 1 ( ) 1 1 ( ) 1 1 cs i sc j ← − ← (i j < ) 2

为Givens矩阵(初等旋转矩阵),也记作T,=T,(c,s)。由Givens矩阵 所确定的线性变换称为Givens变换(初等旋转变换)。 说明:(1)实数c2+s2=1,故存在0,使c=cos(0),s=sin(0)。 (2)y=Tx中T,确定了将向量x变成y的一种变换,正是Givens 袋2-a9 确定的正是平面直角坐 标系中绕原点的一个旋转变换(旋转日度)。 (3)以上实Givens矩阵也可推广称为复初等旋转矩阵。 3
为 Givens 矩阵(初等旋转矩阵),也记作 (,) T T cs ij ij = 。由 Givens 矩阵 所确定的线性变换称为 Givens 变换(初等旋转变换)。 说明:(1)实数 2 2 c s + =1,故存在θ ,使c s = = cos( ), sin( ) θ θ 。 (2) ij y Tx = 中Tij 确定了将向量 x 变成 y 的一种变换,正是 Givens 变换。二阶情况下, cos( ) sin( ) sin( ) cos( ) y x θ θ θ θ = − 确定的正是平面直角坐 标系中绕原点的一个旋转变换(旋转θ 度)。 (3)以上实 Givens 矩阵也可推广称为复初等旋转矩阵。 3

1 1 cele seje ←-(@) 1 Uk= 1 -s j识3 ←-(k) 1 ◆◆· 1 4
1 2 3 4 1 1 ( ) 1 1 ( ) 1 1 ik j j U j j ce se i k se ce θ θ θ θ = ← − ← 4

其中c与s仍为满足c2+s2=1的实数,日,02,0,0,为实角度。 显然,det(U)=c2e8+8)+s2e+8) 当0+8=82+0,时,det(Uk)=e4+8 当8+04=02+03=2nm时,det(Uk)=1 2.性质 (1)[T,(c,s)]=[T,(c,s)]=T,(c,-),-s=-sin(e=sin-8), 旋转0度再反向旋转度0 detT,(c,s)=1 (2)设x=[552…5n],y=Tx=[☑h2…],则有 5
其中 c 与 s 仍为满足 2 2 c s + =1的实数, 1234 θθ θθ ,,, 为实角度。 显然, 1 4 2 3 2 2 ( ) ( ) det( ) j j U ce se ik θ θ+ θ θ+ = + 当θθ θ θ 14 23 +=+ 时, 1 4 ( ) det( ) j U e ik θ θ+ = 当 14 23 θθ θ θ π +=+= 2n 时,det( ) 1 Uik = 2. 性质 (1) 1 (,) (,) (, ) T T cs T cs T c s ij ij ij − = = − , − =− = − s sin( ) sin( ) θ θ , 旋转θ 度再反向旋转度θ det , 1 ( ) T cs ij = (2)设 [ 1 2 ] T n x = ξξ ξ , [ 1 2 ] T ij n y Tx = = ηη η ,则有 5