
第一章复数与复变函数 By 付小宁
第一章 复数与复变函数 By 付小宁

§1复数及代数运算 1.复数的概念 回顾历史,瑞士数学家欧拉(Euler,1707~1783)在前人确信负数开方能 施行的基础上于1737年第一次提出用i表示-1的平方根.因为这种数不是直接 产生于计算或测量,所以相对于实数,人们很自然地称它为虚数.这样,数的概 念在实数的基础上进一·步得到发展,产生了复数与复变量.为了进一步研究复变 量之间的依赖关系,德夙数学家高斯(Gauss,1777-1855)于1811年正式引入 了复变函数的概念,法国数学家柯西(Cauchy,1789~1857)给出了柯西-黎曼 方程,于1814年建立起复变函数的积分理论,提供了计算留数公式,复变函数 的级数理论是德国数学家魏尔斯特拉斯 (Weierstrass, 1815-1897)在191世纪 初建立的,德国数学家黎曼(Reimann, 1826一1866)在19世纪对复变函数的 几何理论作出了很大贡献, 由于生产实际问题的需要,复变函数理论从19世纪以来得到了差勃的发展, 它不仅与其他学科(如理论物理,自动控制等)有着密切的联系,而且与数学中 其他分支有着密切的联系,我国数学家陈景润(1933一1996)在研究“哥德巴赫 猜想”问题中就广泛应用了复变函数的理论.正因为复变函数有如此广泛的联系 与应用,所以学好这门课就显得很有必要
1. 复数的概念 §1 复数及代数运算
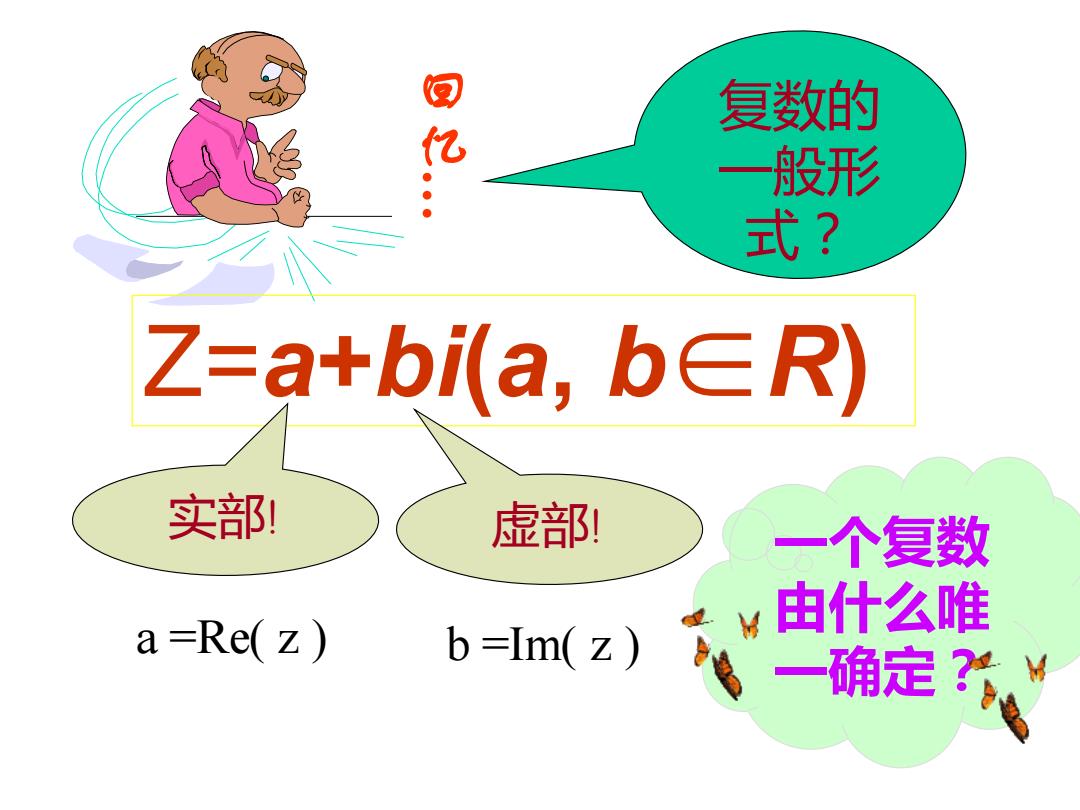
复数的 亿 般形 式? Z=a+bi(a,b∈R) 实部! 虚部! 一个复数 由什么唯 a -Re(z b =Im(z) 一确定
回 忆 … 复数的 一般形 式? Z=a+bi(a, b∈R) 实部! 虚部! 一个复数 由什么唯 一确定? a =Re( z ) b =Im( z )
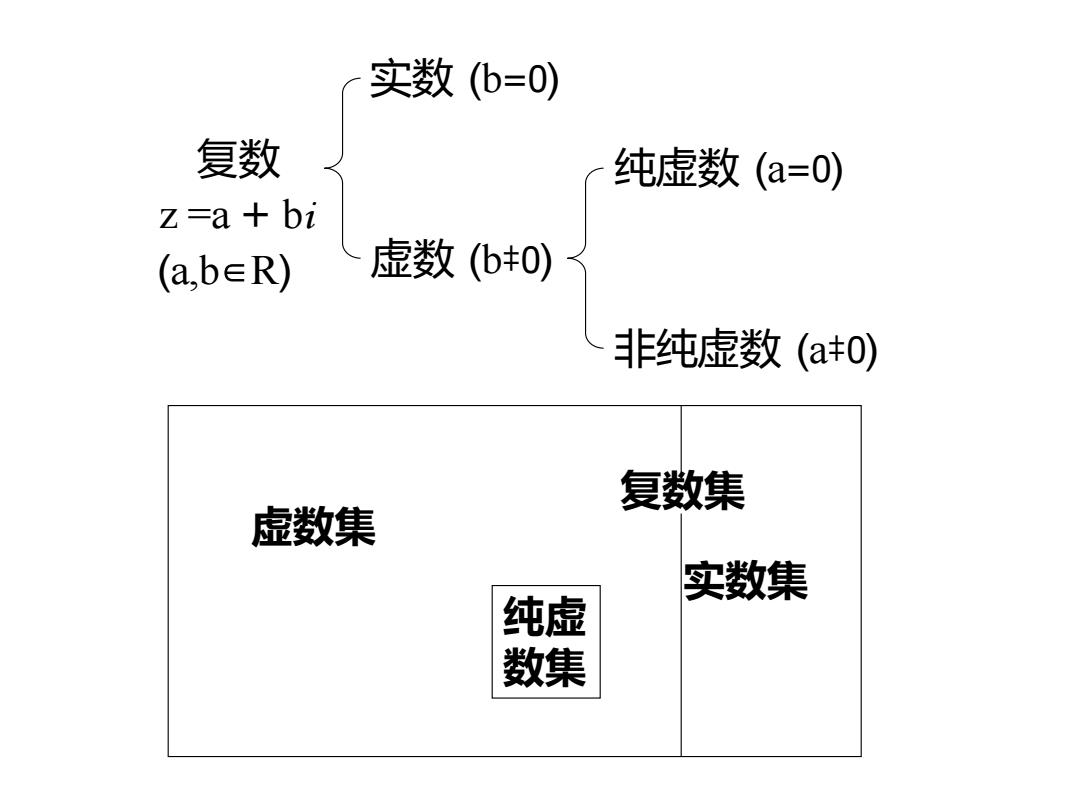
实数(b=0) 复数 纯虚数(a=0) z =a bi (a,beR) 虚数(b0) 非纯虚数(ao) 复数集 虚数集 实数集 纯虚 数集
复数 z =a + bi (a,b∈R) 实数 (b=0) 虚数 (b‡0) 纯虚数 (a=0) 非纯虚数 (a‡0) 虚数集 纯虚 数集 复数集 实数集

复数的概念 复数不能比较大小的一种解释 例如:与0能不能比较大小? (1)如果i>0,那么i>0i,即-1>0。 (2)如果i<0,那么i>0,(←)2>0(-) 即-1>0. 因此,与0不能比较大小。 Note Z1=a1+ib1,Z2 =a2+ib2 Z1=Z2 if a=az bi=b2
复数不能比较大小的一种解释 (1)如果i>0,那么i·i>0·i,即-1>0。 (2)如果i<0,那么-i>0,(-i)2>0·(-i) 即-1>0. 例如:i与0能不能比较大小? 因此,i与0不能比较大小。 A 复数的概念 Note Z1 =a1 + i b1 , Z2 =a2 + i b2 Z1 = Z2 if a1= a2 & b1= b2