
第七讲矩阵级数与矩阵函数
第七讲 矩阵级数与矩阵函数 1

一、矩阵序列 1.定义:设有矩阵序列{A},其中A=(a),且当k→oo时 a→a,则称{A}收敛,并把A=(a)叫做{4}的极限,或称 {A}收敛于A,记为 limA=A或A)→A k-oc 不收敛的矩阵序列则称为发散的,其中又分为有界和无界的情况。 对于矩阵序列{A},若存在常数M>0,使得对一切k都有 a<M 则称{4}为有界的。 2
一、 矩阵序列 1. 定义: 设有矩阵序列{ } ( ) k A , 其中 ( ) () () k k A a = ij , 且当 k → ∞ 时 ( ) k ij ij a a → , 则称{ } ( ) k A 收敛, 并把 A a = ( ij) 叫做{ } ( ) k A 的极限, 或称 { } ( ) k A 收敛于 A, 记为 ( ) lim k k A A →∝ = 或 ( ) k k A A →∝ → 不收敛的矩阵序列则称为发散的,其中又分为有界和无界的情况。 对于矩阵序列{ } ( ) k A ,若存在常数M > 0,使得对一切 k 都有 ( ) k ij a M< 则称{ } ( ) k A 为有界的。 2

2.收敛矩阵序列的性质: 设{4},{B}分别收敛于A,B则 ()aA+BB之aA+BB (2)A)B)→AB (3)若(A),A存在,则()→A (4)PAQ→PAg 3收敛矩阵的定义:设A为方阵,若当k→∝时A→0,则称A为收敛 矩阵。 3
2. 收敛矩阵序列的性质: 设 { } ( ) k A ,{ } ( ) k B 分别收敛于 A,B则 (1) () () k k k A B AB →∝ α β αβ + →+ (2) () () k k k A B AB →∝ → (3) 若 () 1 1 ( ), k A A − − 存在,则 () 1 1 ( ) k k A A − − →∝ → (4) ( ) k k PA Q PAQ →∝ → 3 收敛矩阵的定义: 设 A为方阵,若当k →∝时 0 k A → , 则称 A为收敛 矩阵。 3

[定理]方阵A为收敛矩阵的充要条件是A的所有特征值的模值均小于 1. 证明:对任何方阵A,均存在可逆矩阵P,使得 A=PJP- 其中J为A的Jordan标准形 TA 1 0 J2 ,J 2 0
[定理] 方阵 A为收敛矩阵的充要条件是 A的所有特征值的模值均小于 1. 证明: 对任何方阵 A,均存在可逆矩阵P, 使得 1 A PJP− = 其中 J 为 A的 Jordan 标准形 1 2 s J J J J = , 1 0 1 0 i i i i J = λ λ λ 4
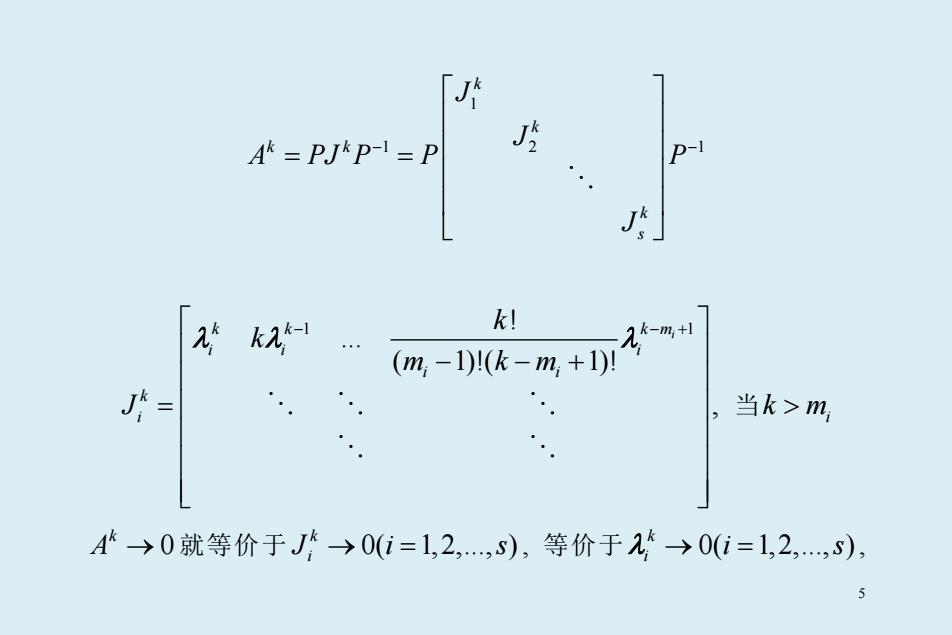
「J Ak=PJKP-=P J P-1 2k2 k! … (m,-1)(k-m,+1)川 J= 。 当k>m A→0就等价于J→0(i=1,2,S),等价于2→0(i=1,2,,)
1 1 1 2 k k k k k s J J A PJ P P P J − − = = 1 1 ! ... ( 1)!( 1)! , i k k k m i i i i i k i k k m km J − − + − −+ = λ λ λ 当 i k m> 0 k A → 就等价于 0( 1,2,..., ) k i Ji s → = , 等价于 0( 1,2,..., ) k i λ → =i s , 5