
第十三讲Penrose广义逆矩阵(I)
第十三讲 Penrose 广义逆矩阵(I) 1

一、Penrose广义逆矩阵的定义及存在性 所谓广义,即推广了原有概念或结果。我们知道,逆矩阵概念是 针对非奇异的(或称为满秩的)方阵。故这一概念可推广到:(1)奇 异方阵;(2)非方矩阵。事实上,Penrose广义逆矩阵涵盖了两种情况。 对于满秩方阵A,A存在,且AA1=AA=I故,当然有 AAA=A AAA=A (AA)=44 (44)=44 这四个对满秩方阵显然成立的等式构成了Penrose广义逆的启示。 2
一、Penrose 广义逆矩阵的定义及存在性 所谓广义,即推广了原有概念或结果。我们知道,逆矩阵概念是 针对非奇异的(或称为满秩的)方阵。故这一概念可推广到:(1)奇 异方阵;(2)非方矩阵。事实上, Penrose 广义逆矩阵涵盖了两种情况。 对于满秩方阵 A, A−1 存在,且 AA−1 =A−1 A=I 故,当然有 -1 -1 -1 -1 -1 -1 -1 () () H H AA A A A AA A AA AA AA AA = = = = 这四个对满秩方阵显然成立的等式构成了 Penrose 广义逆的启示。 2

1.Penrose定义:设A∈Cmx",若Z∈Cmxm且使如下四个等式成立, AZA=A,ZAZ=Z,(AZ)=AZ,(ZA)=ZA 则称Z为A的Moore-Penrose(广义)逆,记为,A。 而上述四个等式又依次称为Penrose方程(i),(i),(ii,(iv)。 2.Moore-Penrose逆的存在性和唯一性 定理:任给A∈Cmx”,AT均存在且唯一。 证明:存在性.廿A∈C,”,均存在西矩阵U∈Cmm,V∈C”使 3
1. Penrose 定义:设 A∈C m n× ,若 Z∈Cn m× 且使如下四个等式成立, AZA = A, ZAZ = Z, (AZ) H = AZ , (ZA) H = ZA 则称 Z 为 A 的 Moore-Penrose(广义)逆,记为,A† 。 而上述四个等式又依次称为 Penrose 方程(i),(ii) ,(iii) ,(iv)。 2. Moore-Penrose 逆的存在性和唯一性 定理:任给 A∈C m n× ,A† 均存在且唯一。 证明:存在性. ∀ A∈C m n r × ,均存在酉矩阵 U∈C m m m × ,V∈Cn n n × 使 3

62 : 0 UHAV=D = 即A=UDVH Or 0 0 mxn 其中,O,o,,o?是A“A的全部非零特征值。 此时,令Z=VDUH∈Cm 则 4
U H AV = D = 1 2 0 0 0 r m n σ σ σ × 即 A = UDV H 其中, 22 2 1 2 , ,, σσ σ r 是 A H A 的全部非零特征值。 此时,令 Z=V ~ DUH ∈Cn m r × 则 4
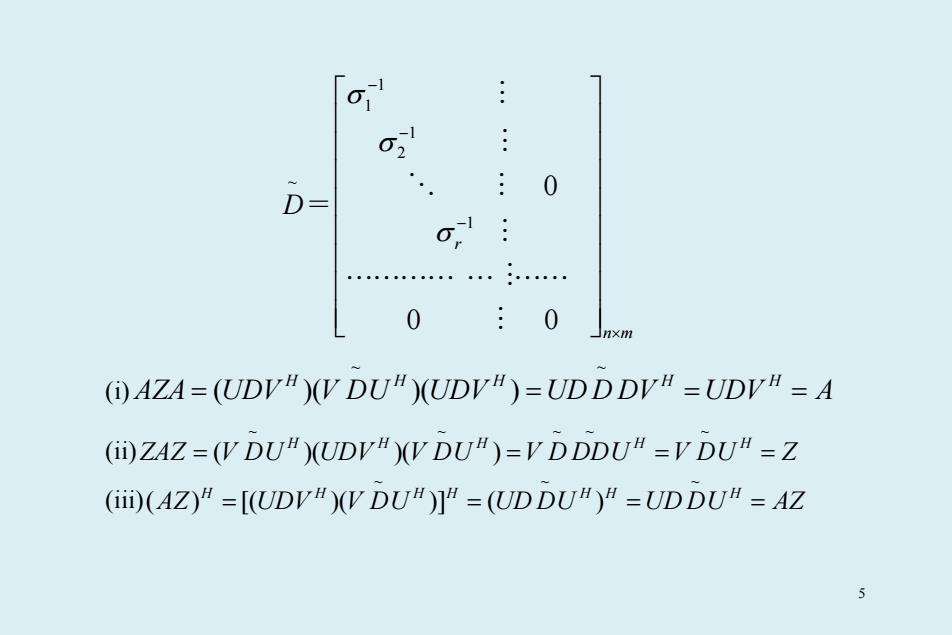
0 D ☐nxm (i)AZA=(UDVH)(V DUR)(UDVA)=UDDDVH =UDVH=A (ii)ZAZ=(V DUH)(UDVH)(V DUH)=V DDDU#=V DU=Z (iii)(AZ)H=[(UDV)(V DUR)]H=(UD DUR)H=UD DUH=AZ 5
~ D= 1 1 1 2 1 0 0 0 r n m σ σ σ − − − × (i) ~ ~ ( )( )( ) H HH H H AZA UDV V DU UDV UD D DV UDV A = = = = (ii) ~ ~ ~ ~ ~ ( )( )( ) HH H H H ZAZ V DU UDV V DU V D DDU V DU Z = = = = (iii) ~ ~~ ( ) [( )( )] ( ) H H H H H H H AZ UDV V DU UD DU UD DU AZ = = = = 5