
第十二讲 满秩分解与奇异值分解
第十二讲 满秩分解与奇异值分解 1

一、矩阵的满秩分解 L.定义:设A∈C,m"(>O),若存在矩阵F∈Cm及G∈C,”,使得 A=FG,则称其为A的一个满秩分解。 说明:(1)F为列满秩矩阵,即列数等于秩;G为行满秩矩阵,即行 数等于秩。 (2)满秩分解不唯一。D∈C(r阶可逆方阵),则 A=FG=F(DD)G=(FDD'G)=FG,且F∈C,m',G∈C” 2.存在性定理:任何非零矩阵均存在满秩矩阵 证明:采用构造性证明方法。设A∈C,”,则存在初等变换矩阵 E∈C", 2
一、矩阵的满秩分解 1. 定义:设 ( 0) m n AC r r × ∈ > ,若存在矩阵 m r F Cr × ∈ 及 r n G Cr × ∈ ,使得 A FG = ,则称其为 A的一个满秩分解。 说明:(1)F 为列满秩矩阵,即列数等于秩;G 为行满秩矩阵,即行 数等于秩。 (2)满秩分解不唯一。 r r D Cr × ∀ ∈ (r 阶可逆方阵),则 1 1 1 1 A FG F DD G FD D G FG ( ) ( )( ) − − = = = = ,且 1 1 , mr rn FC GC r r × × ∈ ∈ 2. 存在性定理:任何非零矩阵均存在满秩矩阵 证明:采用构造性证明方法。设 m n A Cr × ∈ ,则存在初等变换矩阵 m m E Cm × ∈ , 2

G1r行 使EA=B= 其中G∈C 0(m-r)行 将A写成A=EB,并把E分块成E=[F|S],其中 r列(m-r)列 F∈Cm =FG 是满秩分解。 3.Hermite标准形(行阶梯标准形) 3
使 ....... ( ) G r EA B O mr = = − 行 行 , 其中 r n G Cr × ∈ 将 A写成 1 A EB− = ,并把 1 E− 分块成 [ ] 1 ( ) | r mr EFS − − = 列 列 ,其中 m r F Cr × ∈ . . .... . G A F S FG O ∴ = = 是满秩分解。 3. Hermite 标准形(行阶梯标准形) 3

设B∈Cm"(r>O),且满足 (1) B的前r行中每一行至少含一个非零元素(称为非零行), 且第一个非零元素为1,而后(m-r)行的元素全为零(称为 零行): (2) 若B中第i行的第一个非零元素(即1)在第j,列 (i=1,2,,r),则 方<j2<.<j, (3) 矩阵B的第j列,第j2列,,第j,列合起来恰为m阶单位 方阵Im的前r列(即j2,,j列上除了前述的1外全为0) 则称B为Hermite标准形。 4
设 ( 0) m n BC r r × ∈ > ,且满足 (1) B的前r 行中每一行至少含一个非零元素(称为非零行), 且第一个非零元素为 1,而后( ) m r − 行的元素全为零(称为 零行); (2) 若 B 中 第 i 行的第一个非零元素(即 1 )在第 i j 列 ( 1,2,..., ) i r = ,则 1 2 ... r jj j < << ; (3) 矩阵B的第 1 j 列,第 2j 列,…,第 rj 列合起来恰为m阶单位 方阵 m I 的前r 列(即 1 2 , ,..., r jj j 列上除了前述的 1 外全为 0) 则称B为 Hermite 标准形。 4
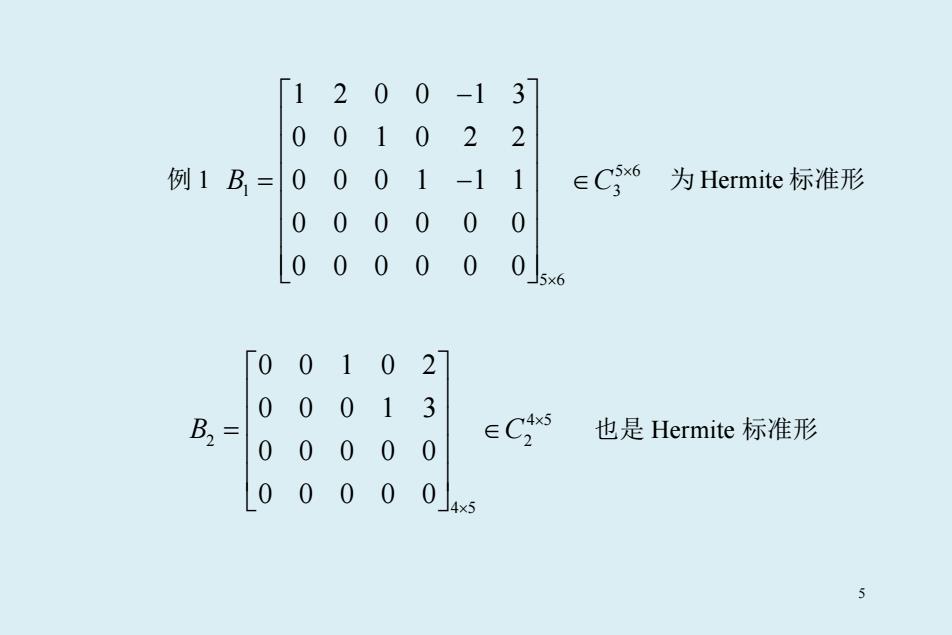
[1200-1 3 0 0102 2 例1B1= 0001-11 ∈C36 为Hermite标准形 000000 L00000 0 5×6 0 0102 0 001 3 B2 也是Hermite标准形 0 0 00 0 00 00 x5 5
例 1 5 6 1 3 5 6 1200 13 0010 2 2 0001 11 0000 0 0 0000 0 0 B C × × − = − ∈ 为 Hermite 标准形 4 5 2 2 4 5 00102 00013 00000 00000 B C × × = ∈ 也是 Hermite 标准形 5