
第四讲矩阵的对角化
第四讲 矩阵的对角化 1
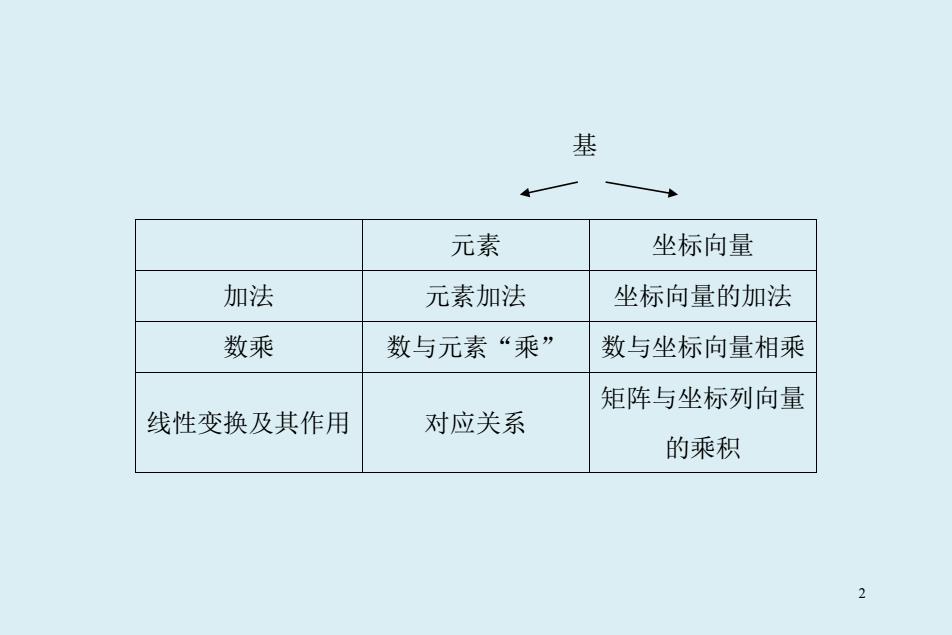
基 元素 坐标向量 加法 元素加法 坐标向量的加法 数乘 数与元素“乘” 数与坐标向量相乘 矩阵与坐标列向量 线性变换及其作用 对应关系 的乘积 2
基 元素 坐标向量 加法 元素加法 坐标向量的加法 数乘 数与元素“乘” 数与坐标向量相乘 线性变换及其作用 对应关系 矩阵与坐标列向量 的乘积 2

对任何线性空间,给定基后,我们对元素进行线性变换或线性运 算时,只需用元素的坐标向量以及线性变换的矩阵即可,因此,在后 面的内容中着重研究矩阵和向量。 3
对任何线性空间,给定基后,我们对元素进行线性变换或线性运 算时,只需用元素的坐标向量以及线性变换的矩阵即可,因此,在后 面的内容中着重研究矩阵和向量。 3

对角矩阵的形式比较简单,处理起来较方便,比如求解矩阵方程 Ax=b时,将矩阵A对角化后很容易得到方程的解。对角化的过程实 际上是一个去耦的过程。以前我们学习过相似变化对角化。那么,一 个方阵是否总可以通过相似变化将其对角化呢?或者对角化需要什么 样的条件呢?如果不能对角化,我们还可以做哪些处理使问题变得简 单呢?
对角矩阵的形式比较简单,处理起来较方便,比如求解矩阵方程 Ax b = 时,将矩阵 A对角化后很容易得到方程的解。对角化的过程实 际上是一个去耦的过程。以前我们学习过相似变化对角化。那么,一 个方阵是否总可以通过相似变化将其对角化呢?或者对角化需要什么 样的条件呢?如果不能对角化,我们还可以做哪些处理使问题变得简 单呢? 4

一、特征值与特征向量 1.定义:对m阶方阵A,若存在数入,及非零向量(列向量)x,使 得Ax=入x,则称入为A的特征值,x为A的属于特征值2的特 征向量。 ·特征向量不唯一 。特征向量非零 (λI-A)x=0有非零解,则det(2I-A)=0,称det(λI-A) 为A的特征多项式
一、 特征值与特征向量 1. 定义:对m阶方阵 A,若存在数λ ,及非零向量(列向量) x ,使 得 Ax x = λ ,则称λ 为 A的特征值,x为 A的属于特征值λ 的特 征向量。 • 特征向量不唯一 • 特征向量非零 • ( )0 λI Ax − = 有非零解,则det( ) 0 λI A − = ,称det( ) λI A − 为 A的特征多项式。 5