
第十七讲矛盾方程(组)的解--最小二乘法
第十七讲 矛盾方程(组)的解---最小二乘法 1
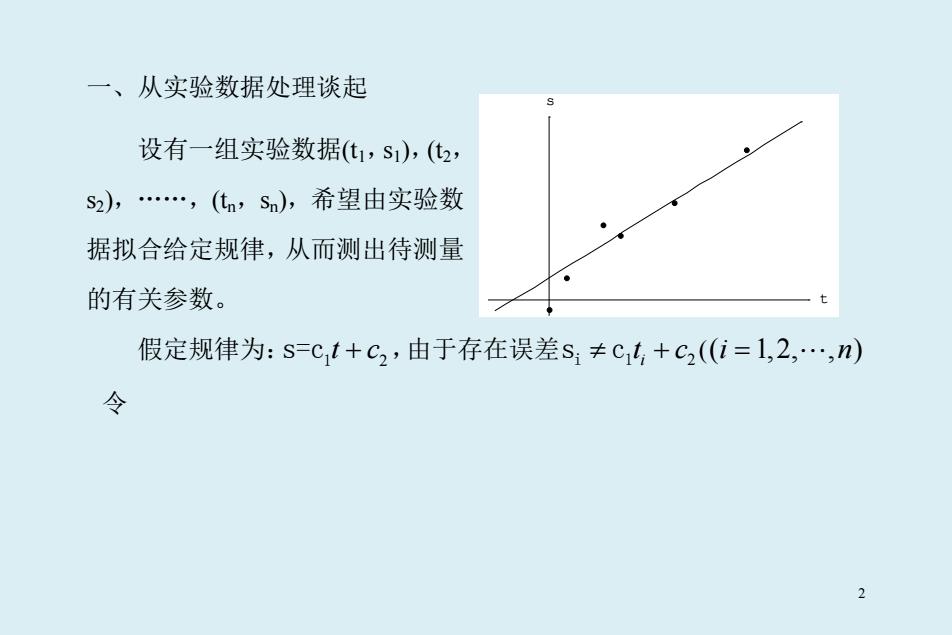
一、从实验数据处理谈起 设有一组实验数据t1,s1),(2, S2),…,(n,Sn),希望由实验数 据拟合给定规律,从而测出待测量 的有关参数。 假定规律为:s=Ct+C2,由于存在误差S1≠C4+C2(i=1,2,…,n) 令 2
一、从实验数据处理谈起 设有一组实验数据(t1,s1),(t2, s2),……,(tn,sn),希望由实验数 据拟合给定规律,从而测出待测量 的有关参数。 假定规律为: 2 s=c1t c + ,由于存在误差 i 2 ≠ + t c i 1 s c (( 1,2, , ) i n = 令 t s 2

A= 则:Ax=b实际无解,或者说矩阵 方程Ax=b成为矛盾方程(不自洽、非相容),虽说无解,但在物理上 看,我们需要而且也理当有“解”。怎么办? 一 般处理是,定义一种目标函数,例如: E(G,9)=∑w(s-c4-c2)2 w,>0为加权系数 使误差E(c,S)最小化。w=1=1~n)时E(G,c)广Ax-b6 3
1 1 2 2 1 2 1 1 , , 1 n n t s t s c A xb c t s = = = ,则:Ax=b 实际无解,或者说矩阵 方程 Ax=b 成为矛盾方程(不自洽、非相容),虽说无解,但在物理上 看,我们需要而且也理当有“解”。怎么办? 一般处理是,定义一种目标函数,例如: 2 1 2 1 2 1 (, ) ( ) 0 n ii i i i E c c w s ct c w = = −− > ∑ 为加权系数 使误差 1 2 Ec c (, )最小化。wi=1(i=1~n)时 2 1 2 2 E c c Ax b (, )= − 3

二、最小二乘法(解) 对于矛盾方程Ax=b,最小二乘法是求其“解”的一种方法。即求 使Ax-bl2=min的解。 引理:设A∈Cmx”,A{1,3}由如下方程的通解构成: AX=A43)→A1,3}={A3)+(I-A3》A)ZZ∈Cm} 其中,A1,3)为A{1,3}中的某个矩阵。 证:1·方程既然相容,设X是其某个解,则 (①)AXA=AA,3)A=A→X∈A{1 (i)(AX)H=(AA13)H=AA1,3)=AX→X∈A3} 4
二、 最小二乘法(解) 对于矛盾方程 Ax=b,最小二乘法是求其“解”的一种方法。即求 使 Ax b − =2 min的解。 引理: m n A C × 设 ∈ ,A{1,3}由如下方程的通解构成: (1,3) (1,3) (1,3) {1,3} { ( ) } n m AX AA A A I A A Z Z C × = → = +− ∈ 其中,A(1,3)为 A{1,3}中的某个矩阵。 证:1。 方程既然相容,设 X 是其某个解,则 (1,3) (1,3) (1,3) ( ) {1} ( ) ( ) ( ) {3} H H i AXA AA A A X A iii AX AA AA AX X A = =→∈ = = = →∈ 4

即方程的解必在A{1,3}中。 2设X为A的一个{1,3}-逆矩阵,则 AX=AAAX=(A3)(AX)月 =(4)”AXA =(43)“(AX4A) =(AAL3)”=A43) 即,A的{1,3}-逆矩阵必满足方程AX=AA1,3) 5
即方程的解必在 A{1,3}中。 2 。 设 X 为 A 的一个{1,3}-逆矩阵,则 ( ) ( ) ( ) ( ) ( ) iii (1,3) (1,3) (1,3) (1,3) (1,3) (1,3) ( ) H H H H HH H H H AX AA AX AA AX A AX A A AXA AA AA = = = = = = 即,A 的{1,3}-逆矩阵必满足方程 AX=AA(1,3) 5