
3.3微分中值定理 第二章 单变量函数的微分学 极值与极值点 定义:设函数f(x)在x的邻域B(x,6)=(x-6,x。+6)上有定义, 若f(x)≥f(x)(x∈B(x,δ),则称f(x)为f(x)的 极大值;x是f(x)的极大值点 类似可定义极小值与极小值点, 极大值 极大值点 极值 极值点 极小值 极小值点 注:(1)极大值、极小值可以有很多个: (2)极大值未必大于极小值; (3)极值点必须在区间内部;与函数连续性、可导性无关, 2
2 3.3 微分中值定理 第二章 单变量函数的微分学 定义:设函数 在 的邻域 上有定义, 若 0 x 0 0 0 B x( , ) ( , ) x x 则称 为 的 极大值; 是 的极大值点. 0 x 类似可定义极小值与极小值点. 极值 极大值 极小值 极值与极值点 注:(1) 极大值、极小值可以有很多个; (2) 极大值未必大于极小值 ; (3) 极值点必须在区间内部;与函数连续性、可导性无关. 极值点 极大值点 极小值点

3.3微分中值定理 第二章】 单变量函数的微分学 定理(Fermat):若(I)x,为f(x)的极值点(2)f(x)在x,可导, 则'(x)=0. f'(x)=0 定义:称导数为0 的点为驻点. 驻点是可能的极值点. 证明:不妨设x,为极大值点. f(xo)=f (xo)=lim f(x+△)-f(x≤0 △x→0 △x f"(xo)=f(x)=lim f(+△)-f(x ≥0 x-20 △x →f'(xo)=0. 3
3 3.3 微分中值定理 第二章 单变量函数的微分学 0 f x ( ) 0. 定理(Fermat):若 ( )1 x0 为 的极值点 在 x0 可导, 则 x y O 0 x 0 f x ( )=0 ' 0 0 0 0 0 ( ) ( ) ( ) ( ) lim 0 x f x x f x f x f x x ' 0 0 0 0 0 ( ) ( ) ( ) ( ) lim 0 x f x x f x f x f x x 证明:不妨设 x0 为极大值点. 0 f x ( ) 0. 定义: 称导数为0 的点为驻点. 驻点是可能的极值点
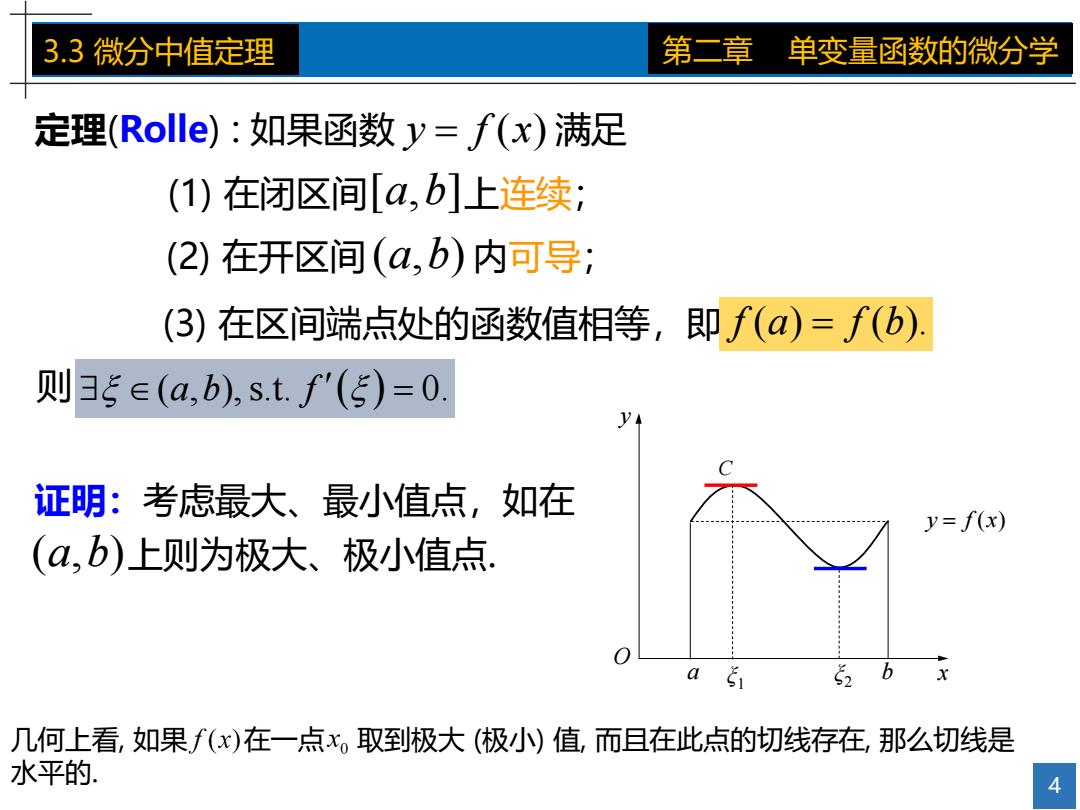
3.3微分中值定理 第二章 单变量函数的微分学 定理(Rolle):如果函数y=f(x)满足 (1)在闭区间[a,b]上连续; (2)在开区间(a,b)内可导; (3)在区间端点处的函数值相等,即f(a)=f(b). 则35∈(a,b),s.tf'(5)=0. 证明:考虑最大、最小值点,如在 y=f(x) (a,b)上则为极大、极小值点. 0 几何上看,如果f(x)在一点x,取到极大(极小小)值,而且在此点的切线存在,那么切线是 水平的. 4
4 3.3 微分中值定理 第二章 单变量函数的微分学 定理(Rolle) : 如果函数 y f x ( ) 满足 (1) 在闭区间 [ , ] a b 上连续; (2) 在开区间 ( , ) a b 内可导; 则 (3) 在区间端点处的函数值相等,即 f a f b ( ) ( ). ( , ), s.t. 0. a b f O x y C a ξ b 1 ξ2 y f x ( ) 几何上看, 如果 在一点 取到极大 (极小) 值, 而且在此点的切线存在, 那么切线是 水平的. 证明:考虑最大、最小值点,如在 ( , ) a b 上则为极大、极小值点

3.3微分中值定理 第二章 单变量函数的微分学 定理(Rolle):如果函数y=f(x)满足 (1)在闭区间[a,b]上连续; 3个条件缺一不可. (2)在开区间(a,b)内可导;。。o (3)在区间端点处的函数值相等,即f()=f(b). 则35∈(a,b),s.tf'(5)=0. 三个条件之一不满足时结论不成立的反例: f(x)=x f(x) f(x)=x (1) (2) (3) 5
5 3.3 微分中值定理 第二章 单变量函数的微分学 O 1 1 y f x x ( ) y 1 O 1 f x x ( ) O 1 1 y f x( ) (1) (2) (3) 3个条件缺一不可. 定理(Rolle) : 如果函数 y f x ( ) 满足 (1) 在闭区间 [ , ] a b 上连续; (2) 在开区间 ( , ) a b 内可导; 则 (3) 在区间端点处的函数值相等,即 f a f b ( ) ( ). ( , ), s.t. 0. a b f 三个条件之一不满足时结论不成立的反例:

3.3微分中值定理 第二章 单变量函数的微分学 1:证明x3-3x+c=0在(0,1)中不可能有两相异实根. 2:f(x)=x(x-1)…(x-100),则f'(x)=0有 个实根 3:若实系数多项式f(x)的根全为实根,则f'(x)的根也全是实的. 6
6 3.3 微分中值定理 第二章 单变量函数的微分学 3: 若实系数多项式 f x( ) 的根全为实根,则 f x ( ) 的根也全是实的. 2: f x x x ( ) ( 1) ( 100), x 则 f x ( ) 0 有______个实根. 1: 证明 在 中不可能有两相异实根. 3 x 3 0 x c (0,1)