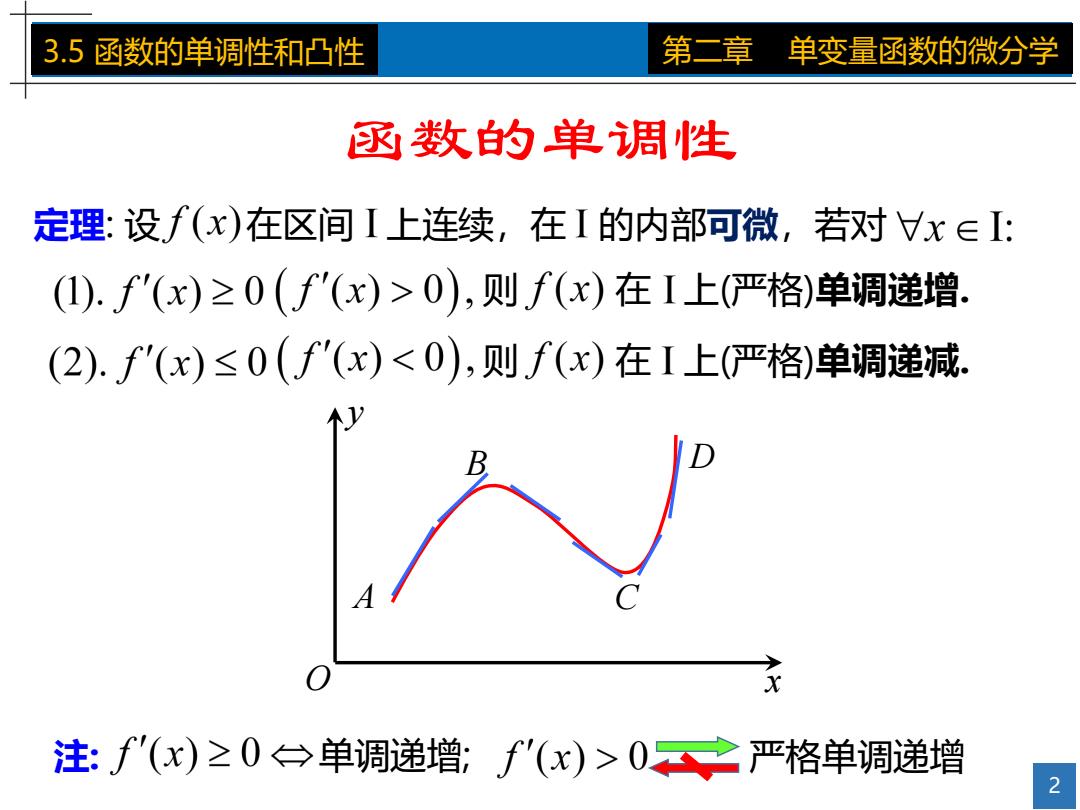
3.5函数的单调性和凸性 第二章 单变量函数的微分学 逐数的单调性 定理:设f(x)在区间I上连续,在I的内部可微, 若对Vx∈I: (1).f'(x)≥0(f'(x)>0),则f(x)在I上(严格)单调递增, (2).f'(x)≤0(f'(x)<0),则f(x)在I上(严格)单调递减, 注:∫'(x)≥0台单调递增;f'(x)>0之严格单调递增 2
2 3.5 函数的单调性和凸性 第二章 单变量函数的微分学 定理: 设 在区间 上连续,在 的内部可微,若对 函数的单调性 则 在 上(严格)单调递增. 则 在 上(严格)单调递减. O y x B D A C 注: 单调递增; 严格单调递增

3.5函数的单调性和凸性 第二章 单变量函数的微分学 极值点 定理:设函数f(x)在xo的一个去心邻域内可导,且在x,连续 ① 如果f(x)在x,左边的某个区间(x,-6,xo)内有f'(x)>0, 而在右边的某个区间(x,x+δ)内有f'(x)<0,则x, 为一个极大值点: ②1 如果f(x)在xo左边的某个区间(x,-δ,x,)内有f'(x)<0! 而在x右边的某个区间(x,x+δ)内有f'(x)>0,则x, 为一个极小值点 ③如果f(x)在x,左、右的某个区间内,f'(x)的符号相同,则 Xo不是极值点. 3
3 3.5 函数的单调性和凸性 第二章 单变量函数的微分学 定理: 设函数 在 的一个去心邻域内可导,且在 连续. ③ 如果 在 左、右的某个区间内, 的符号相同, 则 ① 如果 在 左边的某个区间 内有 而在 右边的某个区间 内有 则 为一个极大值点. ② 如果 在 左边的某个区间 内有 而在 右边的某个区间 内有 则 为一个极小值点. 不是极值点. 极值点
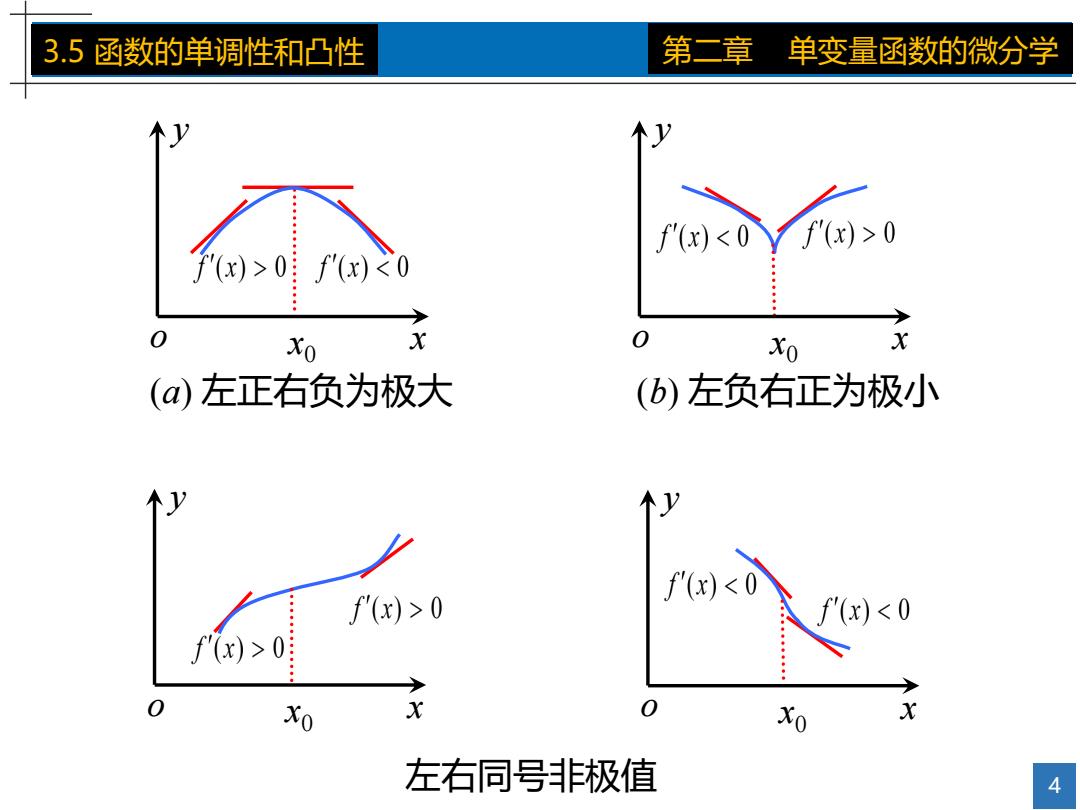
3.5函数的单调性和凸性 第二章 单变量函数的微分学 f(x)>0 f'(x)父0 Xo X 0 Xo X (a)左正右负为极大 (b)左负右正为极小 f'(x)<0 f'(x)>0 f<0 f'x)>0 → Xo X 0 Xo X 左右同号非极值 4
4 3.5 函数的单调性和凸性 第二章 单变量函数的微分学 (a) 左正右负为极大 o y x x 0 o y x x 0 (b) 左负右正为极小 o y x x 0 o y x x 0 左右同号非极值

3.5函数的单调性和凸性 第二章! 单变量函数的微分学 定理:设函数f(x)在x二阶可导,x是f(x)的一个驻点(f'(x)=0) ①如果f"(x,)<0,则x是函数的极大值点; ②如果f"(x,)>0,则x是函数的极小值点. 例.求函数f(x)=x3-3x2-9x+5在区间[-4,4]上的最大值 与最小值. 如何求单变量 函数的最值? 如何证明 例.证明:当0<x≤ 2 函数不等式留 时,有二x≤sinx.o0 2 π 5
5 3.5 函数的单调性和凸性 第二章 单变量函数的微分学 定理: 设函数 在 二阶可导, 是 的一个驻点 ② 如果 则 是函数的极小值点. ① 如果 则 是函数的极大值点; 例. 求函数 在区间 上的最大值 与最小值. 如何求单变量 函数的最值? 例. 证明: 当 时,有 如何证明 函数不等式?

3.5函数的单调性和凸性 第二章 单变量函数的微分学 2 x 例:求证:e*>1+x+ ,x>0. 2! 例:设函数f(x)在[a,+oo)上可导,f(a=0,且当x≥a时有 |f'(x)≤f(x)川.求证:f(x)≡0. 例(Young不等式):设0,B是正数,且0x+B=1.对任意正数 x,y有x“y≤x+By. 6
6 3.5 函数的单调性和凸性 第二章 单变量函数的微分学 例: 求证: 有 例: 设函数 在 上可导, 且当 时有 求证: 例(Young不等式): 设 是正数,且 对任意正数