
中国斜空我术大学 University of Seience and Technology of China Mathematics Analysis Bl 数学科学学院 张明波 mbzhang@ustc.edu.cn 育創 2022年9月 嚴濟感 天下 寰宇 英 學 题 才府
1 前 言 第一章 极限 Mathematics Analysis B1 数学科学学院 张明波 2022年9月 mbzhang@ustc.edu.cn
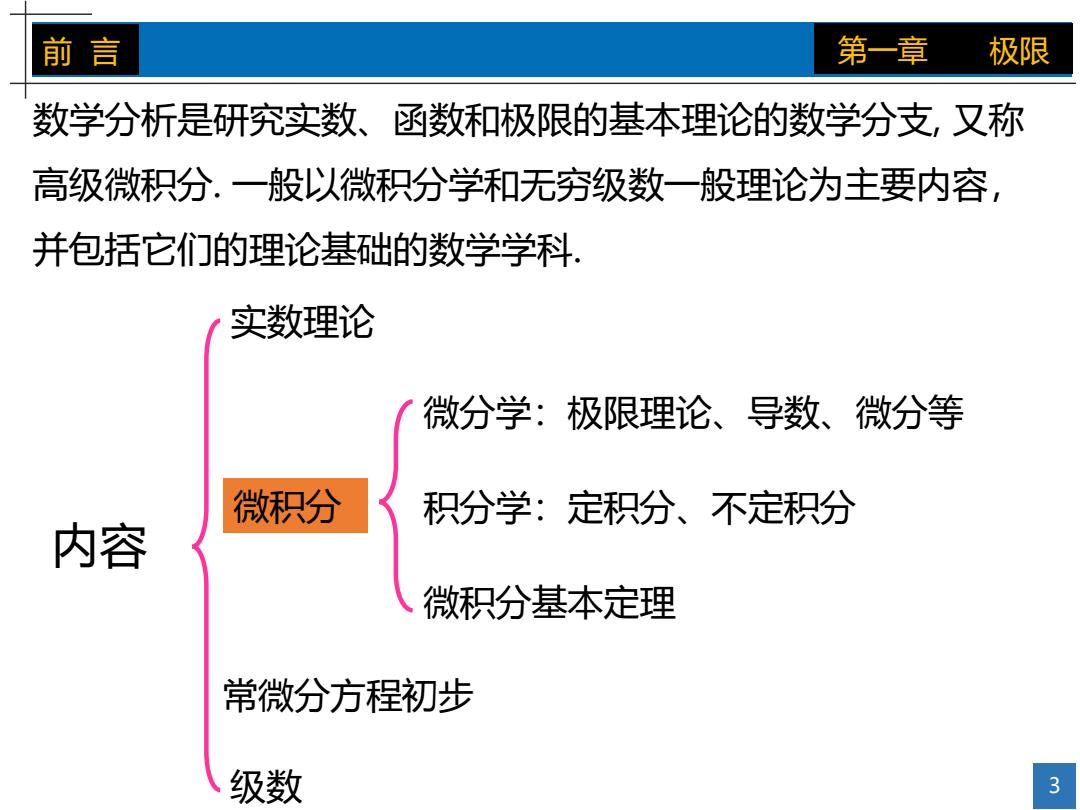
前言 第一章 极限 数学分析是研究实数、函数和极限的基本理论的数学分支,又称 高级微积分.一般以微积分学和无穷级数一般理论为主要内容, 并包括它们的理论基础的数学学科. 实数理论 微分学:极限理论、导数、微分等 微积分 积分学:定积分、不定积分 内容 微积分基本定理 常微分方程初步 级数 3
3 前 言 第一章 极限 内容 微分学:极限理论、导数、微分等 积分学:定积分、不定积分 微积分基本定理 数学分析是研究实数、函数和极限的基本理论的数学分支, 又称 高级微积分. 一般以微积分学和无穷级数一般理论为主要内容, 并包括它们的理论基础的数学学科. 级数 微积分 常微分方程初步 实数理论

前言 第一章 极限 微积分的萌芽 古代数学家的极限、积分思想 朴素、典型 ◆割圆术(魏晋刘徽) 的极限概念 ◆一尺之棰,日取其半,万世不竭(《庄子杂篇天下》) ◆圆周率、球体积、球表面积的研究 (祖冲之、祖暅) ◆号 穷竭法(Euclid,《几何原本》) ◆某些曲线或曲面围成的面积(Archimedes) 5
5 前 言 第一章 极限 古代数学家的极限、积分思想 ◆ 割圆术(魏晋刘徽) ◆ 圆周率、球体积、球表面积的研究(祖冲之、祖暅) ◆一尺之棰,日取其半,万世不竭(《庄子·杂篇·天下》) 朴素、典型 的极限概念 微积分的萌芽 ◆ 穷竭法(Euclid,《几何原本》) ◆ 某些曲线或曲面围成的面积(Archimedes )

前言 第一章 极限 Archimedes(阿基米德287B.c.-212B.C.)--穷竭法 问题:计算弓形(抛物线与直线BC围成)的面积 B 阿基米德的想法是用无数个三角形去逼近这个弓形,他发现: 每次新画的三角形的面积都是上一轮三角形面积的1/4. △ABC· 6
6 前 言 第一章 极限 阿基米德的想法是用无数个三角形去逼近这个弓形,他发现: Archimedes(阿基米德 287 B.C. --212 B.C. )---穷竭法 每次新画的三角形的面积都是上一轮三角形面积的1/4. 问题:计算弓形(抛物线与直线BC围成)的面积

前言 第一章 极限 刘徽(225.-295)--割圆术 问题:计算圆周率(圆周长),R=1. 割之弥细 失之弥少 割之又割 以至于不可割 则与圆合体 而无所失矣 4n:正3.2”边形的边长.→a1=V2-√4-(4=1) 至正24576边形时得到:3.1415926<π<3.1415927 7
7 前 言 第一章 极限 刘徽(225. --295)---割圆术 问题:计算圆周率(圆周长) 正 边形的边长. 至正24576边形时得到: