
反常积分 第五章 单变量函数的积分学 反常积分的概念和计算 积分限有限 常义积分的限制 ↓推广 被积函数有界 反常积分(广义积分) 一、无穷限的反常积分 二、无界函数的反常积分 2
2 反常积分 第五章 单变量函数的积分学 二、无界函数的反常积分 常义积分的限制 积分限有限 推广 被积函数有界 一、无穷限的反常积分 反常积分 (广义积分) 反常积分的概念和计算
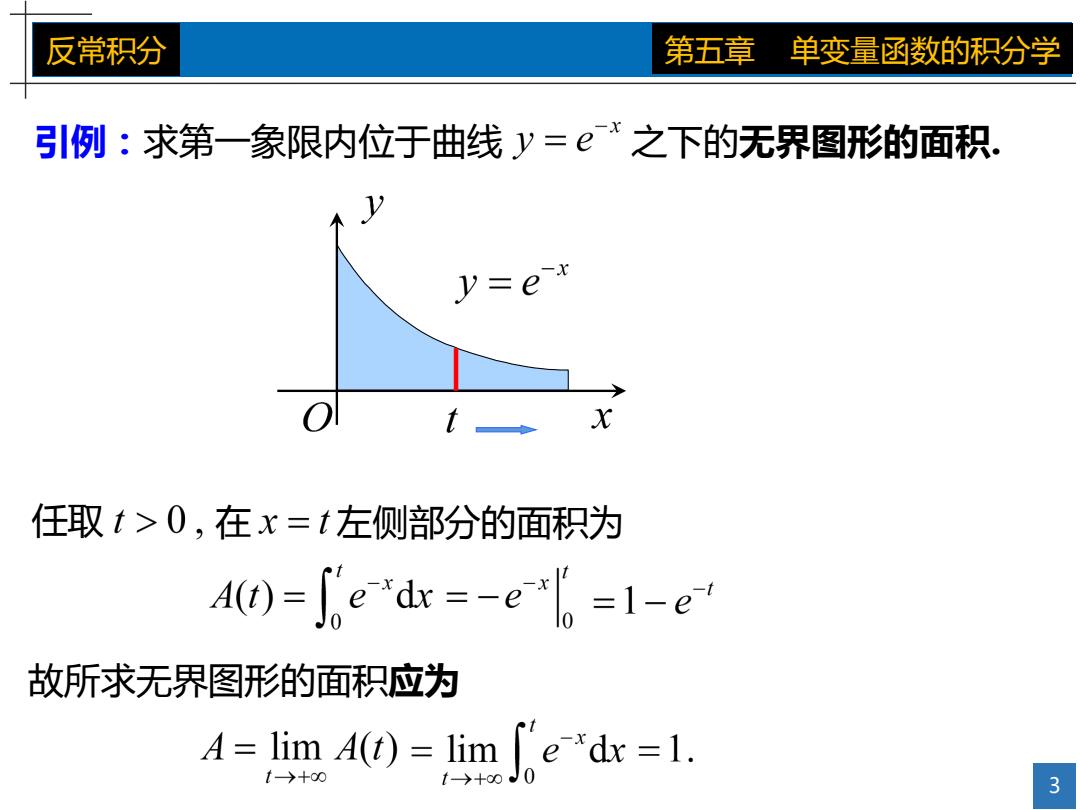
反常积分 第五章 单变量函数的积分学 引例:求第一象限内位于曲线y=ex之下的无界图形的面积. X 任取t>0,在x=t左侧部分的面积为 A(1)=Se"dx =-e*h =1-e' 故所求无界图形的面积应为 4=lim A(t)=lim e"dx =1. t→+00 3
3 反常积分 第五章 单变量函数的积分学 引例:求第一象限内位于曲线 之下的无界图形的面积. 任取 在 左侧部分的面积为 故所求无界图形的面积应为

反常积分 第五章 单变量函数的积分学 无穷区间的反常积分 定义:(1)设f(x)∈C[a,+o),任取b≥a,若1im°f(x)dx b+00● 存在,则称此极限为(x)的无穷限反常积分,记作 ∫。f(x)dr=limf()dk 这时称反常积分f(x)dx收敛; 如果上述极限不存在,就称反常积分f(x)dx发散. (2)类似地,若f(x)∈C(-0,b],则定义 ∫°fw)de=:lim ["f()dr 4
4 反常积分 第五章 单变量函数的积分学 任取 若 无穷区间的反常积分 定义: (1)设 存在 , 则称此极限为 的无穷限反常积分,记作 这时称反常积分 收敛 ; 如果上述极限不存在, 就称反常积分 发散 . (2)类似地 , 若 则定义

反常积分 第五章 单变量函数的积分学 (3)若f(x)∈C(-0,+o),则定义 ∫rfx)dr=∫.fx)dr+∫f(x)dx 只要有一个极限不存在,就称f(x)dx发散. 上述三种形式的反常积分统称为无穷区间的反常积分. 定义:若imf(x)dr存在,则称之为f(x)dr的Cauchy Cauchy主值积分,记为P.V.f(x)dx. xdx 思考: =0正确吗? 5
5 反常积分 第五章 单变量函数的积分学 则定义 只要有一个极限不存在 , 就称 发散 . 上述三种形式的反常积分统称为无穷区间的反常积分. 定义 : 若 存在,则称之为 的Cauchy Cauchy主值积分,记为 思考: 正确吗?

反常积分 第五章 单变量函数的积分学 引入记号 F(+oo)=lim F(x);F(-oo)=lim F(x) x)+00 则有类似Newton-Leibniz公式的计算表达式: 定理:设f(x)在相应的区间上有原函数F(x),则 if(dr=F(t=F4w))-Fa f0md=r。=Fo)-(-o) ∫fde=Fxt-Fw)-f(-o 6
6 反常积分 第五章 单变量函数的积分学 引入记号 ( ) lim ( ) ; x F F x ( ) lim ( ) x F F x 则有类似Newton-Leibniz公式的计算表达式 : 定理: 设 在相应的区间上有原函数 则