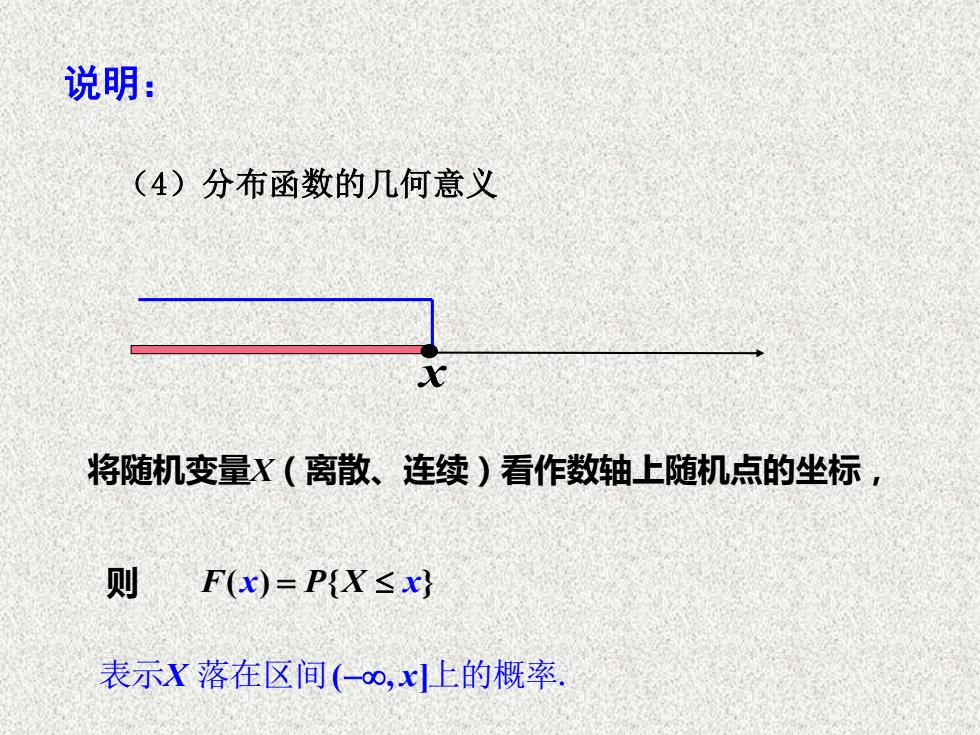
说明: (4)分布函数的几何意义 将随机变量X(离散、连续)看作数轴上随机点的坐标, 则 F(x)=P{X≤x 表示X落在区间(-o,x上的概率
(4)分布函数的几何意义 x 说明: 将随机变量X(离散、连续)看作数轴上随机点的坐标, 表示X x 落在区间( , ] − 上的概率. 则 F P ( ) { } x = X x

说明: Fx)=P{X≤x} (5)若随机变量的分布函数已知,可以求各种随机事件发生 的概率。 P{a<X≤b}=F(b)-F(a) PX≤a=F(a) P(X>a)=1-P(X<a)=1-F(a) P(X<D=PX<B-PIX=b=F(b)-PX=b P(a<X<b)=P(a<X<b)-P(X=DF(b)-F(a)-P(X=b) P{a≤X≤b}=F(b)-F(a)+P{X=d
P a X b { } = − F b F a ( ) ( ) P X a { } = − = − 1 { } 1 ( ) P X a F a = − − = F b F a P X b ( ) ( ) { } P a X b { } P X b { } = − = = − = P X b P X b F b P X b { } { } ( ) { } (5)若随机变量的分布函数已知,可以求各种随机事件发生 的概率。 说明: F P ( ) { } x = X x P X F { } ( ) = a a= { } { } P a X b P X b − = P a X b { } = − + = F b F a P X a ( ) ( ) { }

二、分布函数的性质 (1)F(x)是一个不减函数. 单调不减性 证明:设x1<x2,有F(x2)-F(x) =P{X≤x2}-P{X≤x} =P{x1<X≤x2}≥0,→Fx)≤F(x2)
证明:设 1 2 x x ,有 2 1 F x F x ( ) ( ) − 2 1 = − P X x P X x { } { } 1 2 = P x X x { } 0, 1 2 F x F x ( ) ( ) (1 ( ) )F x 是一个不减函数. 二、分布函数的性质 单调不减性