《线性代数》课程教学课件（PPT讲稿，B）第五章 相似矩阵与二次型_5-4 实对称矩阵的相似对角形

第五章相似矩阵与二次型 4 00 例1设A= 0 3 求正交矩阵P,使P1AP 0 13 为对角形矩阵， 解（①）第一步求4的特征值 4- 0 0 A-AE= 0 3-λ =(2-2)(4-2)2, 0 13- 得特征值入=2,22=入3=4

第五章 相似矩阵与二次型     − − − − = 0 1 3 0 3 1 4 0 0 A E 2 = − − (2 )(4 ) ,   2, 4. 得特征值 1 = 2 = 3 = 1 4 0 0 1 0 3 1 0 1 3 . A P P AP −     =       例 设 ，求正交矩阵 ，使 为对角形矩阵 解 (1)第一步 求A的特征值

第五章相似矩阵与二次型 (2)第二步由(A-2,E)x=0,求特征值对应的特 征向量 0 对2=2，由(A-2E)x=0,得基础解系5= 1 -1 对入2=2=4，由(A-4E)x=0,得基础解系 1 52= 0, 53= 52与5恰好正交， 0 所以51,52,53两两正交

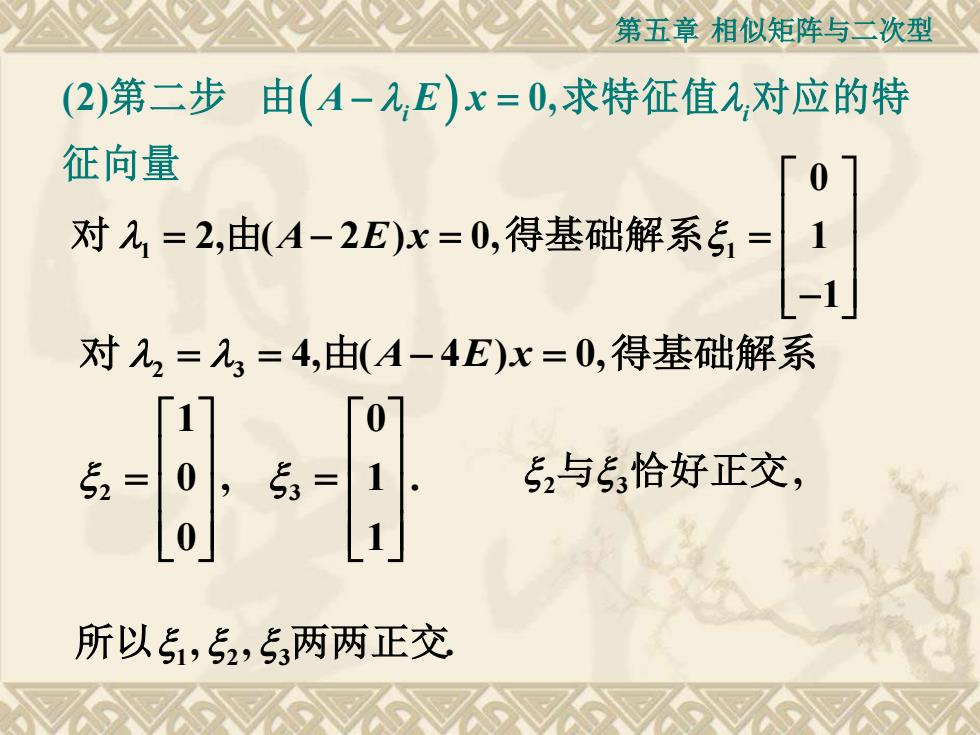
第五章 相似矩阵与二次型 (2) 0, 第二步 由( A E x − =   i i ) 求特征值 对应的特 征向量 1 1 0 2, ( 2 ) 0, 1 1   A E x     = − = =       − 对 由 得基础解系 2 3 2 3 4, ( 4 ) 0, 1 0 0 1 , . 0 1   A E x   = = − =         = =             对 由 得基础解系 ,  2与 3恰好正交 , , . 所以 1  2  3两两正交

第五章相似矩阵与二次型 (3)第三步，再将5,52,5单位化 令==23得 1 0 71= 1/5 ,72= 0,73= 1/W2 -1/W2 o 1/√2

第五章 相似矩阵与二次型 1 2 3 (3) , , , 第三步，再将    单位化 1 2 3 0 0 1 1 2 0 1 2 , , . 1 2 1 2 0                = = =             −       ( 1,2,3) i i i i    令 = = 得