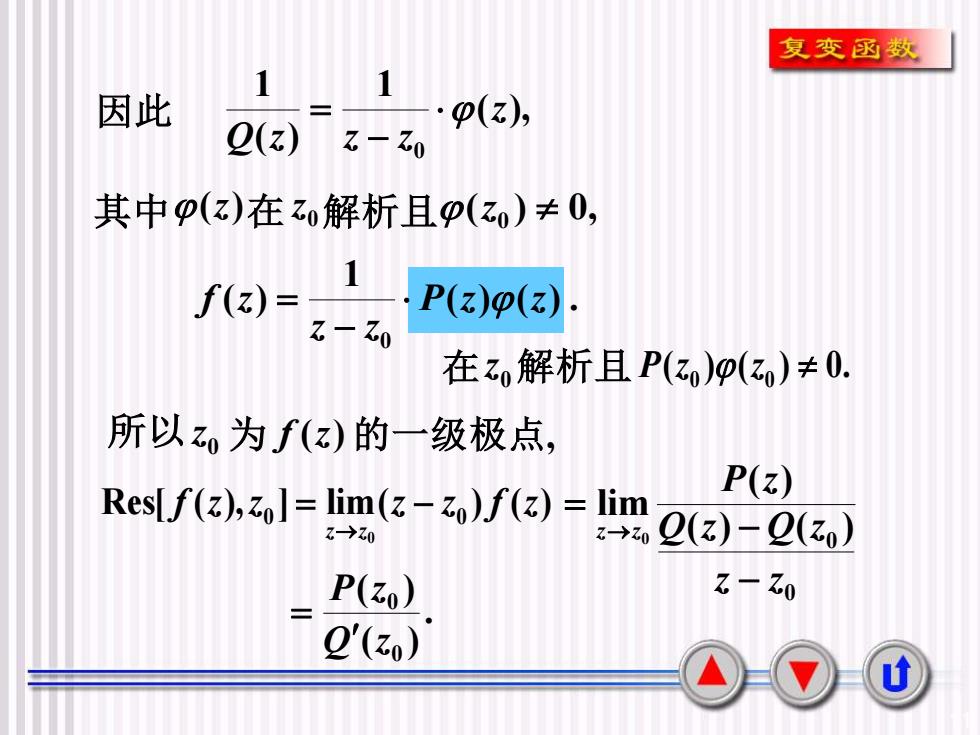
复变函数1因此:p(z),Q(z)Z - zo其中(z)在zo解析且(z)≠ 0,P(z)(z)f(z) =Z - Zo在zo解析且 P(z)(zo)± 0.所以z为f(z)的一级极点,P(z)Res[f(z),zol = lim(z - zo)f(z) = limQ(z) -Q(z)730Z-→Z0Z-ZoP(zo)Q(zo)山
11 z0 解析且 ( ) ( ) 0. 在 P z0 z0 因此 ( ), 1 ( ) 1 0 z Q z z z − = 其中 (z) 在 z0 解析且 ( ) 0, z0 0 所以z 为 f (z) 的一级极点, Res[ ( ), ] lim( ) ( ) 0 0 0 f z z z z f z z z = − → 0 0 ( ) ( ) ( ) lim 0 z z Q z Q z P z z z − − = → . ( ) ( ) 0 0 Q z P z = ( ) ( ) . 1 ( ) 0 P z z z z f z − =

复变函数三、在无穷远点的留数1. 定义 设函数f(z)在圆环域R<z<+8o内解析C为圆环域内绕原点的任何一条正向简单闭曲线那末积分6.f(z)dz的值与无关,则称此定值2元iC为f(z)在8点的留数,记作 Res[f(z),o] =f(z)dzf(z)dz2元i2元i注意积分路线取顺时针方向说明 Res[,f(z),00]=-C-1u
12 三、在无穷远点的留数 注意积分路线取顺时针方向 = − −1 c 1 Res[ ( ), ] = − − 说明 f z c = − C f z z i ( )d 2 1 记作 − = C f z z i f z ( )d 2 1 Res[ ( ), ] 1.定义 设函数 f (z) 在圆环域 R z + 内解析, C为圆环域内绕原点的任何一条正向简单闭曲线, 那末积分 的值与无关, −1 ( )d 2 1 C f z z i 则称此定值 为 f (z)在点的留数