《复变函数与积分变换》课程教学资源（PPT课件）第五章 留数及其应用 5.2 第二节 留数

复变函数证如图f f(z)dz =f f(z)dz + f f(z)dz +..+ f f(z)dzCCC1C2福Z两边同时除以2元i且.2ZDDf(z)dz +f(z)dz +... f(z)dz2元i2元i2元iGC2C.= Res[ f(z),z]]+ Res[ f(z),z2] + ...+ Res[ f(z),zn]nZI[证毕]Res[f(z),z]即可得=k=1u

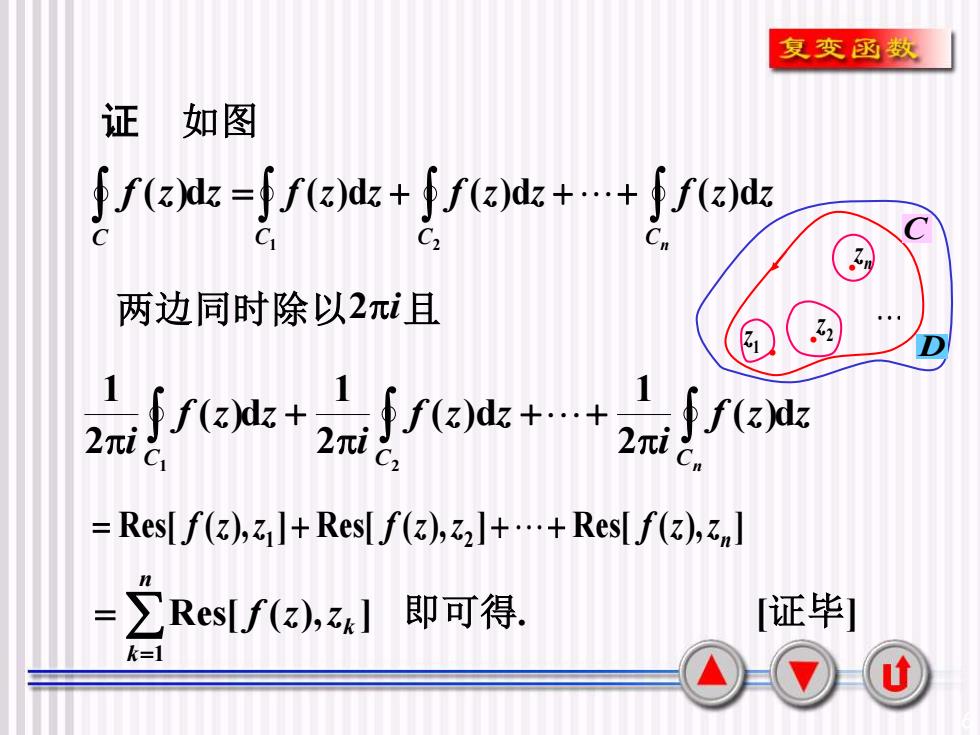
6 证    + + + C C Cn f (z)dz f (z)dz f (z)dz 1 2  f z z =  C ( )d f z z i f z z i f z z i C C Cn ( )d 2 1 ( )d 2 1 ( )d 2 1 1 2     + +  +   Res[ ( ), ] Res[ ( ), ] Res[ ( ), ] 1 2 n = f z z + f z z ++ f z z Res[ ( ), ] . 1  即可得 = = n k k f z z [证毕] 两边同时除以 2i 且 1z 2 z nz D  C . . . 如图

复变函数2.留数的计算方法(1)如果 z为 f(z)的可去奇点，则Res[f(z),ol=0.(2)如果.为f(z)的本性奇点，则需将,f(z)展开成洛朗级数求c-1(3)如果zo为f(z)的极点,则有如下计算规则·规则1如果z为f(z)的一级极点,那末Res[f(z), zol = lim(z - zo)f(z - zo)Z-→Zou

7 2.留数的计算方法 (1) 如果 0 z 为 f (z) 的可去奇点, Res[ ( ), ] 0. 则 f z z0 = Res[ ( ), ] lim( ) ( ). 0 0 0 0 f z z z z f z z z z = − − → •规则1 如果 z0 为 f (z) 的一级极点, 那末 成洛朗级数求 . −1 c (2) 如果 0 z 为 f (z) 的本性奇点, (3) 如果 0 z 为 f (z) 的极点, 则有如下计算规则 则需将 f (z) 展开

复变函数那末·规则2如果zo为f(z)的 m 级极点，dm-11limRes[f(z), zo] =zm-1 [(z - zo)" f(z)].(m - 1)! z-→zo dz证 (z)= C-m(z - zo)-m +...+C_2(z - Zo)-2 ++ c-i(z - zo)-I + Co +C(z - Zo)+..(z-zo)" f(z) =C-m +C-m+1(z-z0)++c-1(z- zo)"-I+ Co(z - Zo)m + Ci(z - Zo)m+1 + ...U

8 如果 z0 为 f (z) 的 m 级极点, [( ) ( )]. d d lim ( 1)! 1 Res[ ( ), ] 1 0 1 0 0 z z f z m z f z z m m m z z − − = − − → •规则2 证 = − + + − + − − − − 2 0 2 0 f (z) c (z z ) c (z z ) m m  + c−1 (z − z0 ) −1 + c0 + c1 (z − z0 ) + 1 0 1 0 1 0 ( ) ( ) ( ) ( ) − − = − + − + − + + − − m m m m z z f z c c z z  c z z + c0 (z − z0 ) m + c1 (z − z0 ) m+1 + 那末

复变函数两边求m-1阶导数dm-1得dzm-l[(z-z0)" (2)=(m-1)!c-l +(含有 z-Zo 正幂的项)dm-1lim[(z - zo)m f(z)] = (m - 1)!c-19z-→zo dzm-1所以 Res[f(z),zo]= c-1dm-11lim[证毕]zm-1[(z - z0)" f(z)].(m -1)! z-zo dzu

9 [( ) ( )] ( 1)! , d d lim 1 0 1 1 0 − − − → z − z f z = m − c z m m m z z 0 1 Res[ ( ), ] = − 所以 f z z c +(含有 z − z0 正幂的项) 1 ( 1)! = − − m c [( ) ( )]. d d lim ( 1)! 1 1 0 1 0 z z f z m z m m m z z − − = − − → [( ) ( )] d d 1 0 1 z z f z z m m m − − − 两边求 m − 1 阶导数, [证毕] 得

复变函数P(z)设f(z)·规则3P(z)及 Q(z)在z.都解析-Q(z)如果 P(z)0,Q(z)=0,Q(z）0，那末z为P(zo)f(z)的一级极点，且有 Res[f(z),zo=Q'(zo)证 因为Q(z)=0,Q(zo)0所以z为 Q(z)的一级零点，zo 为的一级极点，Q(z)u

10 •规则3 如果 ( ) 0, ( ) 0, ( ) 0, P z0  Q z0 = Q z0  设 , ( ) ( ) ( ) Q z P z f z = P(z) 及 Q(z) 在 0 z 都解析， 证 因为Q(z0 ) = 0, Q(z0 )  0 0 所以z 为 Q(z) 的一级零点, ( ) 1 Q z 0 z 为 的一级极点. 那末 0 z 为 的一级极点, f (z) . ( ) ( ) Res[ ( ), ] 0 0 0 Q z P z f z z  且有 =