《复变函数与积分变换》课程教学资源（PPT课件）第九章 拉普拉斯变换（Laplace变换）

复变函数第九章Laplace变换U

第九章 Laplace变换

复变函数Fourier变换的两个限制：(1)定义于[0,+0),而不必考虑t<0时取值的函数(2)绝对可积的条件太强。许多简单函数的傅氏变换或者不存在，或者为非常义下的广义函数给应用带来很大的不方便

2 (1) [0 ), 0 (2) 定义于 ，+   而不必考虑t 时取值的函数； 绝对可积的条件太强。许多简单函数的傅氏 变换或者不存在，或者为非常义下的广义函 数给应用带来很大的不方便。 Fourier变换的两个限制：

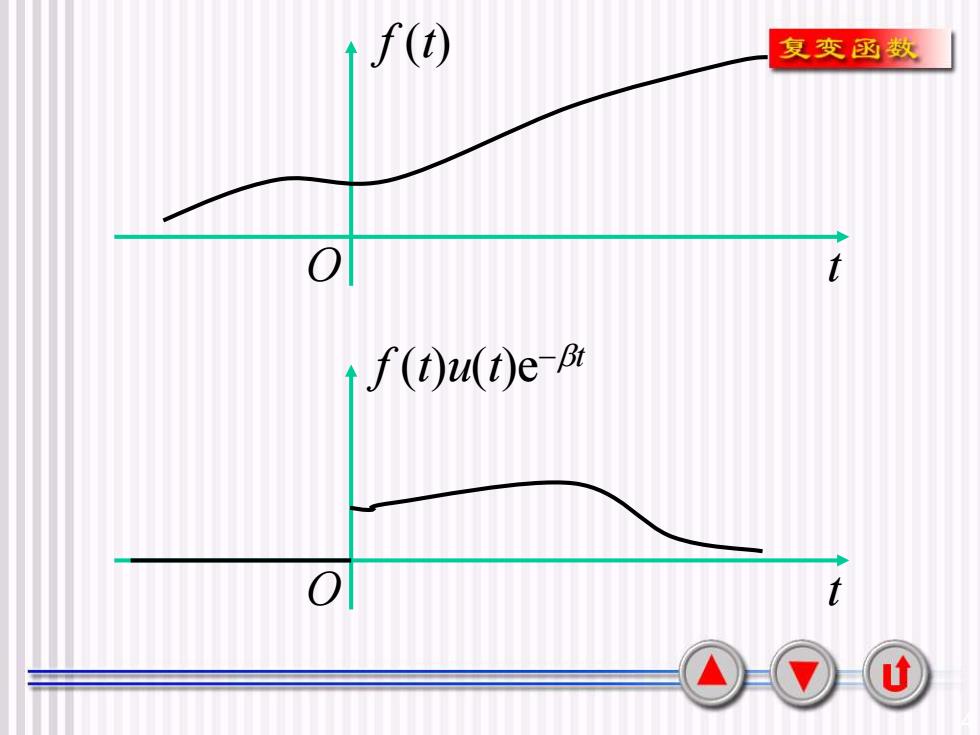
s1Laplace变换的概念复变函数[0,t<o0设指数衰减函数(t)=(β> 0)e-Brt≥0考虑f(t) t E(-0,+o0),有f(t)u(t)=f(t) t≥0.若存在β>0,使 lime-Bif(t)=0,则/e-βtf(t) dt <+oo[->80那磨f(t)u(t)e-βB的傅氏积分总是存在的。F[f(t)u(t)e-B ] = (t f(t)u(t)e-Bte-jot dtS+* f(t)e-(β+jo) dt S=β+ jo f f(t)e-s dtAF(s)U

3 §1 Laplace变换的概念 0, 0 ( ) ( 0). , 0 t t t e t    −   =     设指数衰减函数 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) , 0. 0, lim . t t t t f t t f t u t f t t e f t e f t dt f t u t e      − − →  −  − +    +  + - 考虑 ,有 = 若存在 使 =0,则 那麽 的傅氏积分总是存在的。 ( ) ( ) 0 0 [ ( ) ( ) ] ( ) ( ) ( ) ( ) t t j t j t st f t u t e f t u t e e dt f t e dt s j f t e dt F s        + − − − − + + − + − = = = +     F

f(t)复变函数0f(t)u(t)e-βt01U

4 t f (t) O t f (t)u(t)e−t O

复变函数1.定义：设,f(t)是[0,+o0)上的实(或复)值函数，若对参数s=β+ jO,F(s)=dof(t)e-sdt在s平面的某一区域内收敛，则称其为,f(t)的Laplace变换，记为L[f(t)] = F(s) = (e f(t)e-st dtf(t)称为F(s)的Laplace逆变换，记为f(t)= L'[F(s))F(s)称为像函数，f(t)称为原像函数u

5 ( ) 0 0 1 ( ) [0, ) ( ) , ( ) ( ) ( ) Laplace [ ( )] ( ) ( ) ( ) Laplace ( ) [ ( )]. ( ) ( ) st st f t s j F s f t e dt f t f t F s f t e dt f t F s f t F s F s f t   + − + − − + = + = = = =   设 是 上的实 或复 值函数，若对参数 在s平面的某一区域 内收敛，则称其为 的 变换，记为 称为 的 逆变换，记为 称为像函数， 称为原像函数. L L 1. 定义：