
复变函数于是v,dx+v.dy为某个二元函数y(x,)的全微分,dy(x,y) =-v,dx +Vrdyayay=V-y'axay因为等值线 y(x,y)=c—流线dyVdy(x,j)=-v,dx+Vrdy= 0, 所以dxV场在等值线(x,y)=C上每一点处的向量都与等值线相切函数y(x,)称为场的流函数u
6 流线 , d d ( , ) 的全微分 于是 v x v y为某个二元函数 x y − y + x d (x, y) v dx v dy. = − y + x , . y x v y v x = = − ( , ) , 1 因为等值线 x y = c d (x, y) = −v dx + v dy = 0, y x . d d x y v v x y 所以 = , ( , ) 1 都与等值线相切 场v 在等值线 x y c 上每一点处的向量 v = 函 数 (x, y)称为场v 的流函数.

复变函数2.势函数:如果讠又是B内的无旋场(即势量场)OvyVx=0.即那么rot =0,axay于是vrdx+v,dy为某个二元函数p(x,j)的全微分, dp(x,y)=V,dx +v,dyagagrad@ =.VVaxay函数@(x,J)称为场的势函数(或位函数)等值线戋 (x,y)=c2等势线(或等位线)u
7 2. 势函数: 如果v 又是 B内的无旋场(即势量场), rot v = 0, 那么 = 0. − y v x v 即 y x , d d ( , ) 的全微分 于是 v x v y为某个二元函数 x y x + y d (x, y) v dx v dy, = x + y , . x y v y v x = = grad v. = 函 数 (x, y)称为场v 的势函数(或位函数). ( , ) 等势线(或等位线) 2 等值线 x y = c
复变函数3.平面流速场的复势函数如果在单连域B内,向量场既是无源场又是无旋场,agayayap与同时成立LV三二x,4Vaxayayaxayayap0柯西-黎曼比较后得axaxOyay方程在单连域内可以作一个解析函数平面流速场的复w=f(z)=p(x,y)+iy(x,y)势函数(复势)U
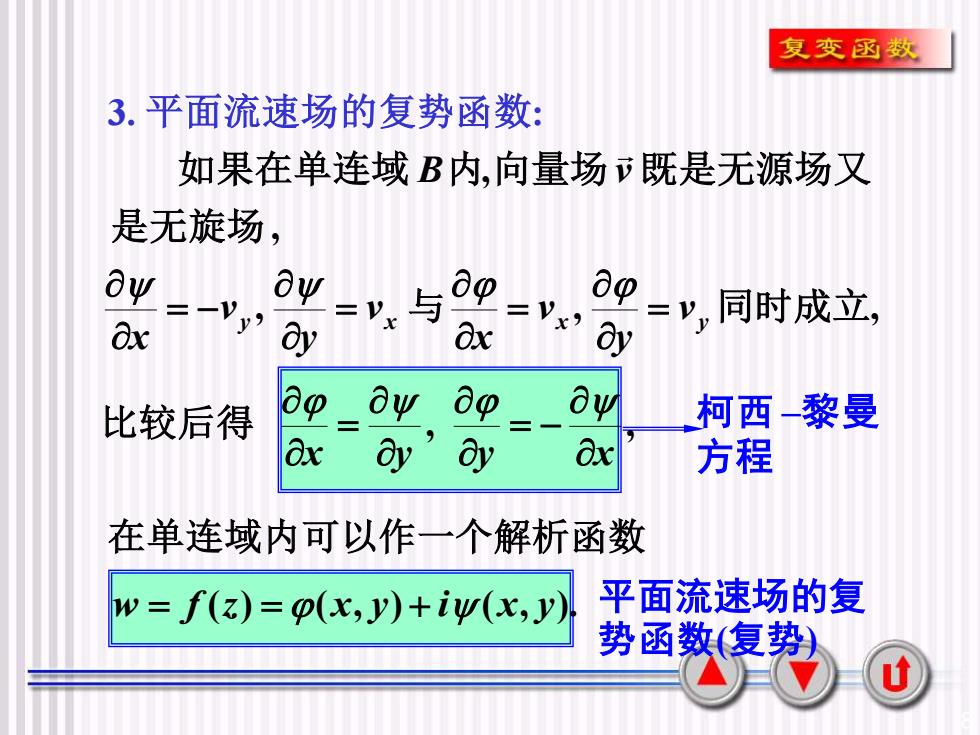
8 平面流速场的复 势函数(复势) 柯西 –黎曼 方程 3. 平面流速场的复势函数: , , 是无旋场 如果在单连域 B内 向量场v 既是无源场又 , 与 y x v y v x = = − , 同时成立, x y v y v x = = , , x y y x = − = 比较后得 在单连域内可以作一个解析函数 w = f (z) = (x, y) + i(x, y)

复变函数agagagay因为 V=Vr+iv,f'(z),-1axayaxax所以流速场可以用复变函数V=f(z)表示给定一个单连域内的无源无旋平面流速场就可以构造一个解析函数一它的复势与之对应;反之,如果在某一区域(不管是否单连)内给定一个解析函数,就有以它为复势的平面流速场对应,并可以写出该场的流函数和势函数,得到流线与等势线方程,画出流线和等势线的图形,即得描绘该场的流动图象u
9 x y 因为 v = v + iv y i x + = x i x − = = f (z), 所以流速场v 可以用复变函数v = f (z)表示. 给定一个单连域内的无源无旋平面流速场, 就可以构造一个解析函数——它的复势与之对 应; 反之, 如果在某一区域(不管是否单连)内给 定一个解析函数, 就有以它为复势的平面流速 场对应, 并可以写出该场的流函数和势函数, 得 到流线与等势线方程, 画出流线和等势线的图 形, 即得描绘该场的流动图象