
上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 2.δ-函数的Fourier变换 -a=咖-ty-北1 & 1,t> 单位阶跃函数 →u'(t-t)=δ(t-to) r[bt-】=J8t-4)erdt=e e 反之,a-4)=r'e]-27Je-da →eo-o'do=2nit-)
2. δ-函数的Fourier变换 0 0 0 0 1, () () 0, t t t t t dt u t t t t δ −∞ > − = −= < ∫ 单位阶跃函数 0 0 ⇒ ut t t t '( ) ( ) −= − δ 0 0 0 0 [ ( )] ( ) it it t t i t t t e t te d e t ω ω ω δ δ +∞ − − − = − ∞ − = − = = ∫ F 2 ( ) 2 1 ( ) [ ] 0 ( ) 1 ( ) 0 0 0 0 e d t t t t e e d i t t i t i t t ⇒ = − − = = ∫ ∫ +∞ −∞ − +∞ −∞ − − − ω πδ ω π δ ω ω ω 反之, F

上游充通大 SHANGHAI JIAO TONG UNIVERSITY 注:引进δ-函数后,可以扩充原像空间与像空间: f(t):f(t)是(-o,+o)上的允许含6-函数 D=了及其导数的实值函数,存在F(o)与f(t) 成为一组Fourier?变换对 F(o):F(o)是(-o∞,+∞)上的允许含δ-函数 R=的F-变换及其导数的复值函数,存在f(t)与F(o 成为一组Fourier?变换对
注:引进δ-函数后,可以扩充原像空间与像空间: − −∞ +∞ − = −∞ +∞ − = 成为一组 变换对 的 变换及其导数的复值函数,存在 与 是 上的允许含 函数 成为一组 变换对 及其导数的实值函数,存在 与 是 上的允许含 函数 Fourier ( ) ( ) ( ): ( ) ( , ) Fourier ( ) ( ) ( ): ( ) ( , ) ω ω ω δ ω δ F f t F F F F f t f t f t R D
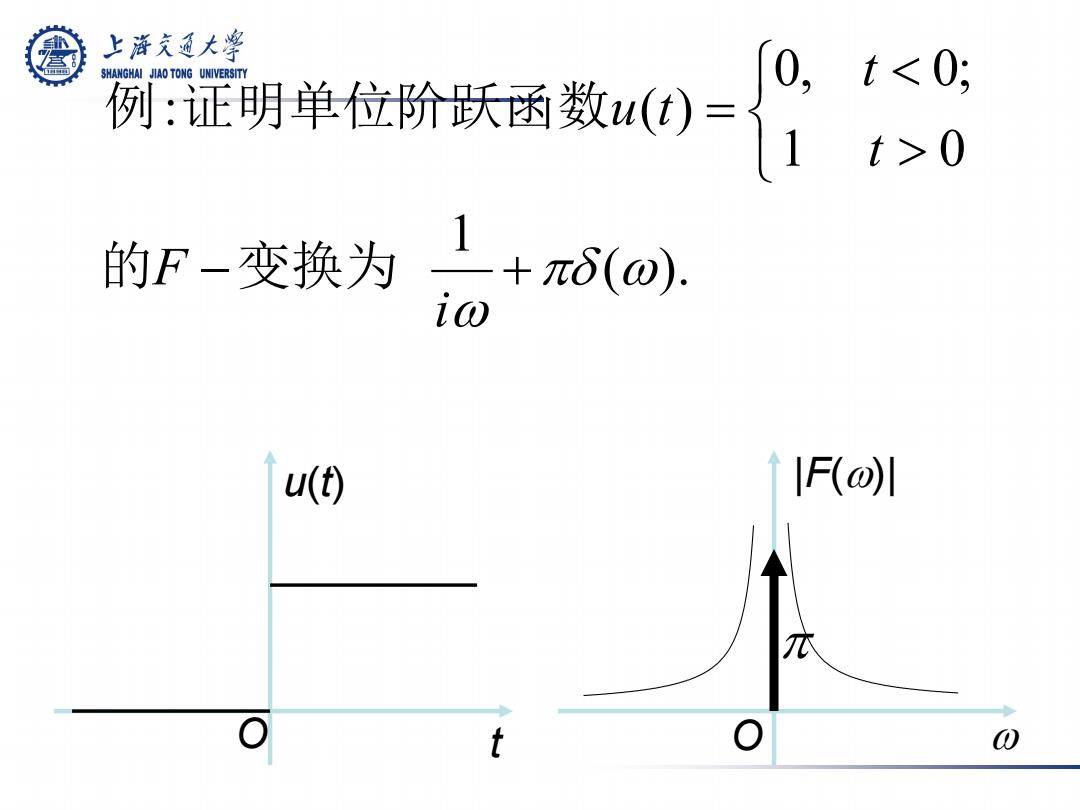
上游充通大学 新明单阶妖函数u0= SHANGHAI JIAO TONG UNIVERSITY 0,t<0: t>0 的F-变换为 .+π6(o) 1) u(t) IF(o训 亦 t 0
( ). 1 1 0 0, 0; : ( ) πδ ω ω − + > < = i F t t u t 的 变换为 例 证明单位阶跃函数 π O ω |F(ω)| O t u(t)

上游充大学 SHANGHAI JIAO TONG UNIVERSITY 证:若F(=,+π6(o)→ iw f(t)=.子-1[F(ω]=u(t) 0yro1oeda do oedw+3a0eaw 2
1 0 1 1 ( ) [ ( )] () d 2 1 1 () d d 2 2 1 1 sin () d d 2 2 1 1 sin d () 2 i t i t i t i t ft F e i e e i t e t u t ω ω ω ω ω πδ ω ω π ω πδ ω ω ω π π ω ω δω ω ω π ω ω ω π ω +∞ − −∞ +∞ +∞ −∞ −∞ +∞ +∞ −∞ −∞ +∞ = = + = + = + = + = ∫ ∫ ∫ ∫ ∫ ∫ F 1 1 () () ( ) [ ( )] ( ) F i f t F ut ω πδ ω ω ω − =+ ⇒ = = 证:若 F
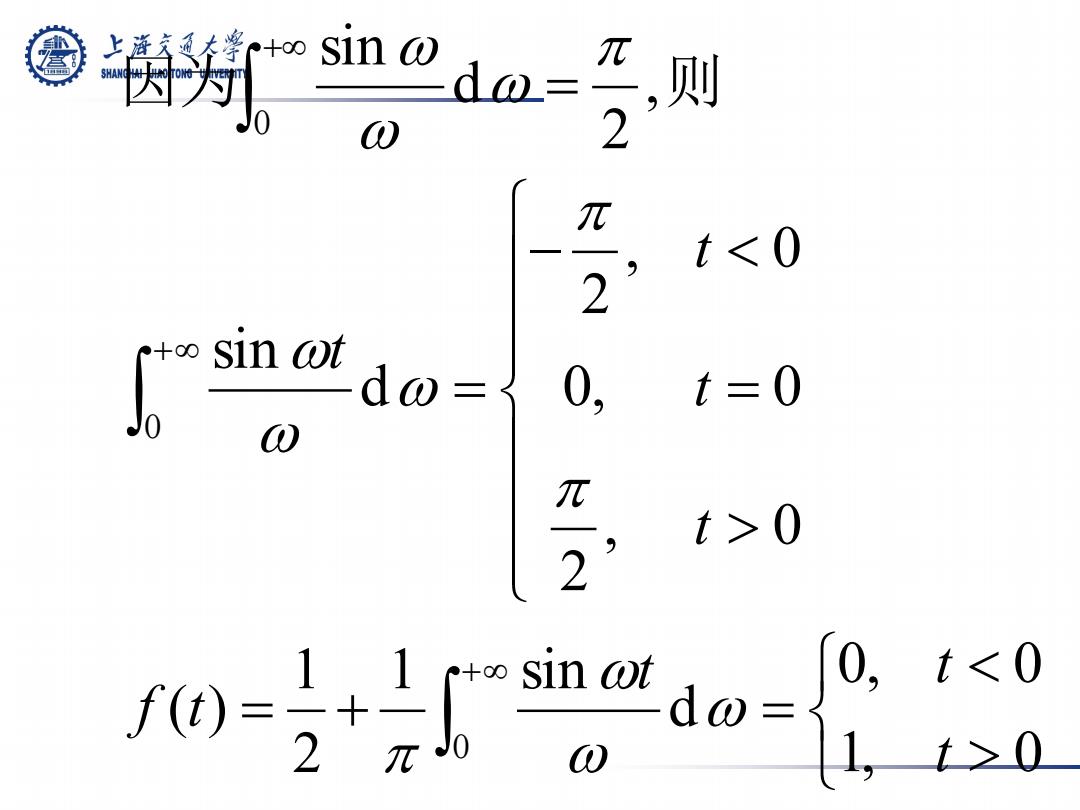
sin wdo 则 O π2 π <0 2 +0 sin at dw 二 0, =0 0 π-2 >0 t 1 0, t<0 2
> < = + = > = − < = = ∫ ∫ ∫ +∞ +∞ +∞ 1, 0 0, 0 d 1 sin 2 1 ( ) , 0 2 0, 0 , 0 2 d sin , 2 d sin 0 0 0 t t t f t t t t t ω ω ω π π π ω ω ω π ω ω ω 因为 则