
第9章图论 第9章图论 91图的基本概念 9.2路和回路 9.3连通图 9.4图的矩阵表示 9.5欧拉图和汉密尔顿图 9.6树 9.7二部图及匹配 9.8平面图 返回总目录
第9章 图论 第9章 图 论 9.1 图的基本概念 9.2 路和回路 9.3 连通图 9.4 图的矩阵表示 9.5 欧拉图和汉密尔顿图 9.6 树 9.7 二部图及匹配 9.8 平面图 返回总目录

第9章图论 第9章图论 图论是一个重要的数学分支。数学家欧拉1736年发 表了关于图论的第一篇论文,解决了著名的哥尼斯堡七 桥问题。克希霍夫对电路网络的研究、凯来在有机化学 的计算中应用了树和生成树的概念。随着科学技术的 发展,图论在运筹学、网络理论、信息论、控制论和计 算机科学等领域都得到广泛的应用。本章首先给出图、 简单图、完全图、子图、路和图的同构等概念,接着研 究了连通图性质和规律,给出了邻接矩阵、可达性矩阵、 连通矩阵和完全关联矩阵的定义。最后介绍了欧拉图与 哈密尔顿图、树、二部图、平面图和图的着色。 返回章目录
第9章 图论 第9章 图论 图论是一个重要的数学分支。数学家欧拉1736年发 表了关于图论的第一篇论文,解决了著名的哥尼斯堡七 桥问题。克希霍夫对电路网络的研究、凯来在有机化学 的计算中都应用了树和生成树的概念。随着科学技术的 发展,图论在运筹学、网络理论、信息论、控制论和计 算机科学等领域都得到广泛的应用。本章首先给出图、 简单图、完全图、子图、路和图的同构等概念,接着研 究了连通图性质和规律,给出了邻接矩阵、可达性矩阵、 连通矩阵和完全关联矩阵的定义。最后介绍了欧拉图与 哈密尔顿图、树、二部图、平面图和图的着色。 返回章目录

第9章图论 9.1图的基本概念 9.1.1图 两个个体x,y的无序序列称为无序对,记为(x,y)。 在无序对(x,y)中,x,y是无序的,它们的顺序可以颠倒, 即(x,y)=(0y,x)。 定义9.1.1图G是一个三重组<G),E(G),0c 其中:(G)是非空结点集。 E(G)是边集。 是边集到结点的有序对或 无序对集合的函数
第9章 图论 9.1图的基本概念 9.1.1图 两个个体x,y的无序序列称为无序对,记为(x,y)。 在无序对(x,y)中,x,y是无序的,它们的顺序可以颠倒, 即(x,y)=(y,x)。 定义9.1.1 图G是一个三重组V(G),E(G),G 其中:V(G)是非空结点集。 E(G)是边集。 G是边集到结点的有序对或 无序对集合的函数
第9章图论 【例9.1】G=<V(G),E(G),pc e 其中:(G)=a,b,c,d E(G)erez.esei PG:Pc(e)(a,b) Pc(e2)-(b,c) e e3 Pc(e:)(a,c) Pc(e)(a,a) b 试画出G的图形。 ez 解:G的图形如图9.1所示。 图9.1
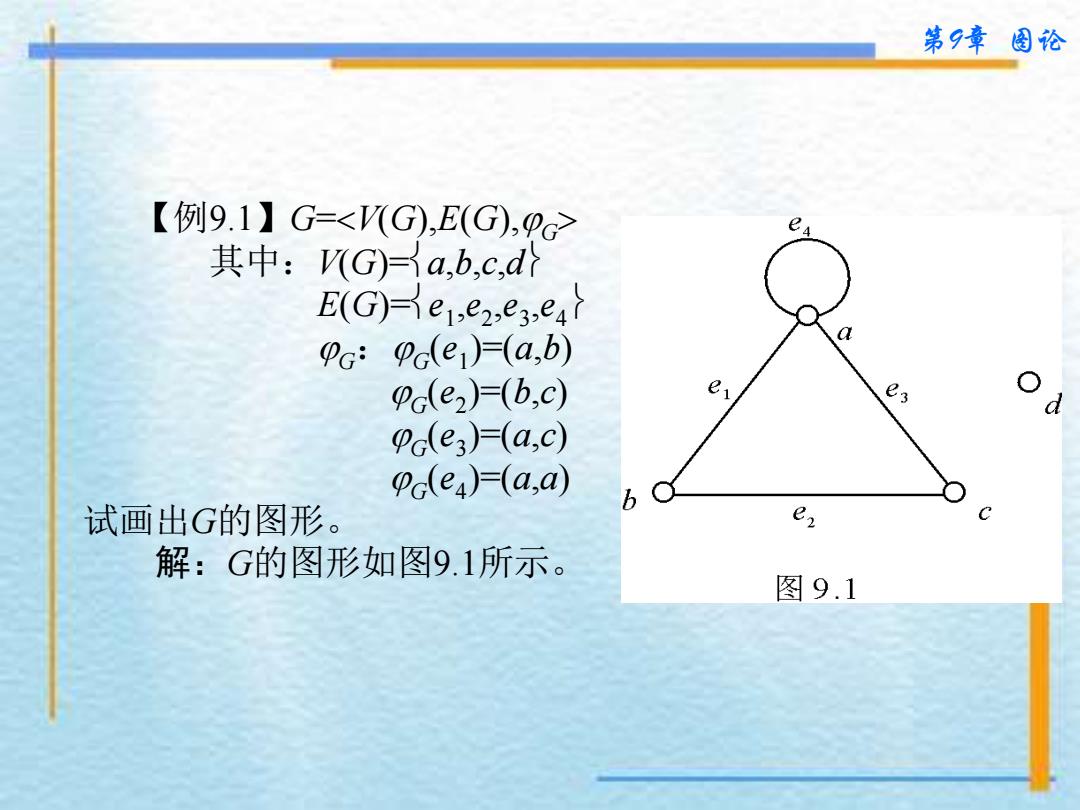
第 9 章 图论 【 例 9 . 1 】 G = V( G), E ( G), G 其中: V( G)= a , b , c , d E ( G)= e 1 , e 2 , e 3 , e 4 G : G ( e 1 )=( a , b ) G ( e 2 )=( b , c ) G ( e 3 )=( a , c ) G ( e 4 )=( a , a ) 试画出 G的图形 。 解: G的图形如图 9 . 1所示

第9章图论 由于在不引起混乱的情况下,图的边可以用有序对或 无序对直接表示。因此,图可以简单的表示为: G=<VE> 其中:V是非空的结点集。 E是边的有序对或无序对组成的集合。 按照这种表示法,例9.1中的图可以简记为: G-<V.E> 其中:a,b,c,d} E=(a,b),(b,c),(a,c),(a,a)}
第9章 图论 由于在不引起混乱的情况下,图的边可以用有序对或 无序对直接表示。因此,图可以简单的表示为: G=V,E 其中:V是非空的结点集。 E是边的有序对或无序对组成的集合。 按照这种表示法,例9.1中的图可以简记为: G=V,E 其中:V=a,b,c,d E=(a,b), (b,c), (a,c), (a,a)